Programming and data structure miscellaneous

Programming and data structure miscellaneous

Easy Questions

Programming & Data Structure

Programming and data structure miscellaneous
  1. Let T (n) be the number of different binary search trees on n distinct elements. Then, 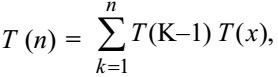where x is








  1. View Hint View Answer Discuss in Forum

    The summation is for each node, if that node happens to be the root. When a node is root, it will have (k – 1) nodes on the left sub tree (k being any number) and correspondingly (n – k) elements on the right sub tree. So, we can write recurrence T (k – 1) * T(n–k) for the number of distinct binary search trees, as the numbers on left and right sub tree from BSTs independent of each other and only a difference in one of the sub trees produces a difference in the tree. Hence answer is B.

    Correct Option: B

    The summation is for each node, if that node happens to be the root. When a node is root, it will have (k – 1) nodes on the left sub tree (k being any number) and correspondingly (n – k) elements on the right sub tree. So, we can write recurrence T (k – 1) * T(n–k) for the number of distinct binary search trees, as the numbers on left and right sub tree from BSTs independent of each other and only a difference in one of the sub trees produces a difference in the tree. Hence answer is B.

  1. Suppose the numbers 7, 5, 1, 8, 3, 6, 0, 9, 4, 2 are inserted in that order into an initially empty binary search tree. The binary search tree uses the usual ordering on natural numbers. What is the in-order traversal sequence of the resultant tree?








  1. View Hint View Answer Discuss in Forum

    We can solve it in shortcut that the first given element in 7, so we need to choose that particular option in which 7 is at the right place i.e. all the elements on its left should be smaller than it & all the elements on the right should be equal & greater than it.
    So this rule is followed in option (c) only. To make in order of a binary search tree.
    (i) Start with the root node.
    (ii) Scan its left subtree,
    (iii) If the node in subtree has any left child then store the node in stack & repeat this step for its left child unit no. left child of any node.
    (iv) If leaf reached then print the node & pop the stack, print the poped value.
    (v) Check its right subtree & repeat step (III) for it.
    (vi) When stack empty then stop
    So here inorder is 0 1 2 3 4 5 6 7 8 9. Actually a fact can be remembered that inorder traversal of a BST leads to a sorted sequence of elements. Hence (c) is correct option.

    Correct Option: C

    We can solve it in shortcut that the first given element in 7, so we need to choose that particular option in which 7 is at the right place i.e. all the elements on its left should be smaller than it & all the elements on the right should be equal & greater than it.
    So this rule is followed in option (c) only. To make in order of a binary search tree.
    (i) Start with the root node.
    (ii) Scan its left subtree,
    (iii) If the node in subtree has any left child then store the node in stack & repeat this step for its left child unit no. left child of any node.
    (iv) If leaf reached then print the node & pop the stack, print the poped value.
    (v) Check its right subtree & repeat step (III) for it.
    (vi) When stack empty then stop
    So here inorder is 0 1 2 3 4 5 6 7 8 9. Actually a fact can be remembered that inorder traversal of a BST leads to a sorted sequence of elements. Hence (c) is correct option.

  1. The following numbers are inserted into an empty binary search tree in the given order: 10, 1, 3, 5, 15, 12, 16. What is the height of the binary search tree (the height is the maximum distance of a leaf node from the root)?








  1. View Hint View Answer Discuss in Forum

    Given are 10, 1, 3, 5, 15, 12, 16

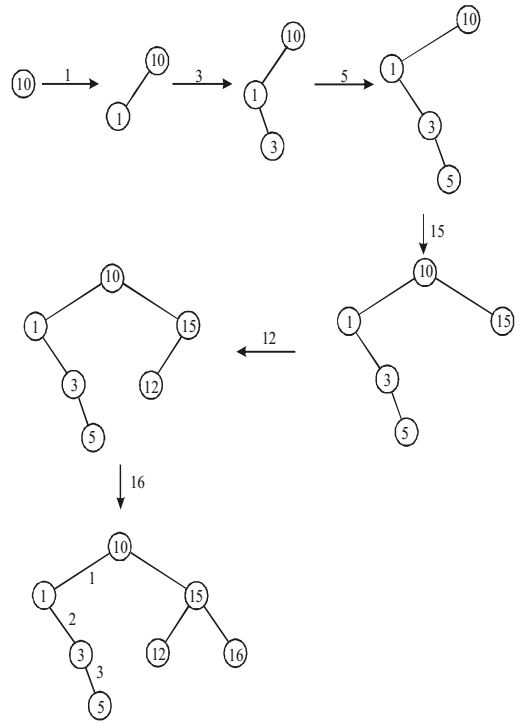
    The height of the leaf node (5) is high 3. Hence (b) is correct option.

    Correct Option: B

    Given are 10, 1, 3, 5, 15, 12, 16

    The height of the leaf node (5) is high 3. Hence (b) is correct option.

  1. Consider the label sequences obtained by the following pairs of traversals on a labelled binary tree. Which of these pairs identify a tree uniquely ?
    (i) Preorder and postorder
    (ii) Inorder and postorder
    (iii) Preorder and inorder
    (iv) Level order and postorder








  1. View Hint View Answer Discuss in Forum

    For a tree we not only require in order & preorder but also postorder traversal.
    Preorder & postorder help to determine the roots of binary subtrees, inorder arranges those roots in order. Hence (b) is correct option.

    Correct Option: B

    For a tree we not only require in order & preorder but also postorder traversal.
    Preorder & postorder help to determine the roots of binary subtrees, inorder arranges those roots in order. Hence (b) is correct option.

  1. A program takes as input a balanced binary search tree with n leaf nodes and computes the value of a function g (x) for each node x. If the cost of computing g (x) is min (number of leaf-nodes in left – subtree of x,number of leaf – nodes in right – subtree of x) then the worst – case time complexity of the program is








  1. View Hint View Answer Discuss in Forum

    At the root node (first level) the cost would be Θ (n/2) as the tree is balanced.
    At next level, we have 2 nodes and for each of them cost of computing g(x) will be Θ (n / 4). So, total cost at second level = Θ (n / 2). Similarly at each level (total cost per level and not the cost per node in a level) the cost would be Θ (n / 2)and so for logn levels it would be Θ (n logn).

    Correct Option: B

    At the root node (first level) the cost would be Θ (n/2) as the tree is balanced.
    At next level, we have 2 nodes and for each of them cost of computing g(x) will be Θ (n / 4). So, total cost at second level = Θ (n / 2). Similarly at each level (total cost per level and not the cost per node in a level) the cost would be Θ (n / 2)and so for logn levels it would be Θ (n logn).