-
Let T (n) be the number of different binary search trees on n distinct elements. Then,
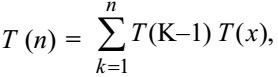where x is
-
- n – k + 1
- n – k
- n – k – 1
- n – k – 2
- n – k + 1
Correct Option: B
The summation is for each node, if that node happens to be the root. When a node is root, it will have (k – 1) nodes on the left sub tree (k being any number) and correspondingly (n – k) elements on the right sub tree. So, we can write recurrence T (k – 1) * T(n–k) for the number of distinct binary search trees, as the numbers on left and right sub tree from BSTs independent of each other and only a difference in one of the sub trees produces a difference in the tree. Hence answer is B.
