Theory of Machines Miscellaneous
- Consider a rotating disk cam and a translating roller follower with zero offset. Which one of the following pitch curves, parameterized by t, lying in the interval 0 to 2π, is associated with the maximum translation of the follower during one full rotation of the cam rotating about the center at (x, y) = (0, 0)?
-
View Hint View Answer Discuss in Forum
From all the four options the maximum amplitudes is in point ‘C’ as t = 0.
(x)t = 0 (y)t = 0
(a) x = 1 y = 0
(b) x = 1 y = 0(c) x = 3 , y = 0 2 (d) x = 3 , y = 0 2
Option ‘c’ has maximum net amplitude.Correct Option: C
From all the four options the maximum amplitudes is in point ‘C’ as t = 0.
(x)t = 0 (y)t = 0
(a) x = 1 y = 0
(b) x = 1 y = 0(c) x = 3 , y = 0 2 (d) x = 3 , y = 0 2
Option ‘c’ has maximum net amplitude.
- In a cam-follower, the follower rises by h as the cam rotates by δ (radians) at constant angular velocity ω (radians/s). The follower is uniformly accelerating during the first half of the rise period and it is uniformly decelerating in the later half of the rise period. Assuming that the magnitudes of the acceleration and deceleration are same, the maximum velocity of the follower is
-
View Hint View Answer Discuss in Forum
Here, out stroke angle θ0 = δ
and stroke length = h
Angular velocity = ω
V = u + at(Vo)max = o + a × t0 = a × δ ......(1) 2 2ω 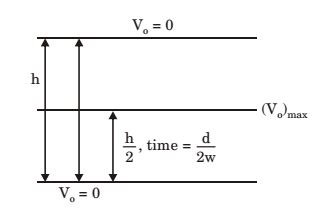
h = O + 1 × a × 
t0 
2 2 2 2 h = aδ2 4ω2 a = 4ω2h .......(2) δ2
From (1) & (2), we get(Vo)max = aδ = 2ωh 2ω δ Correct Option: C
Here, out stroke angle θ0 = δ
and stroke length = h
Angular velocity = ω
V = u + at(Vo)max = o + a × t0 = a × δ ......(1) 2 2ω 
h = O + 1 × a × 
t0 
2 2 2 2 h = aδ2 4ω2 a = 4ω2h .......(2) δ2
From (1) & (2), we get(Vo)max = aδ = 2ωh 2ω δ
- A flat-faced follower is driven using a circular eccentric can rotating at a constant angular velocity ω. At time t = 0, the vertical position of the follower is y(0) = 0, and the system is in the configuration shown below.
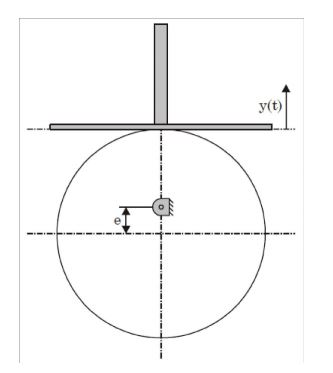
The vertical position of the follower face, y(t) is given by
-
View Hint View Answer Discuss in Forum
As the follower starts moving, the displacement Y can be shown as marked in the diagram
Y = QS – QT
= RU – QT (∵ QS ∥ RU)
= (PR – PU) – QT ...(i)
PR = R'
⇒ PU = e cos θ
QT = (R' – e) from geometry
Now, putting the above values in equation (i) Y = (R' – e cos θ) – (R' – e)
= e – e cos θ
= e(1 – cos θ)
⇒ Y = e(1 – cos ωt) (In time ‘t’,θ = ωt)Correct Option: D
As the follower starts moving, the displacement Y can be shown as marked in the diagram
Y = QS – QT
= RU – QT (∵ QS ∥ RU)
= (PR – PU) – QT ...(i)
PR = R'
⇒ PU = e cos θ
QT = (R' – e) from geometry
Now, putting the above values in equation (i) Y = (R' – e cos θ) – (R' – e)
= e – e cos θ
= e(1 – cos θ)
⇒ Y = e(1 – cos ωt) (In time ‘t’,θ = ωt)
-
In a cam design, the rise motion is given by a Simple Harmonic Motion (SHM) s = h 
1 - cos πθ 
2 β
where h is total rise, θ is camshaft angle, β is the total angle of the rise interval. The jerk is given by
-
View Hint View Answer Discuss in Forum
The jerk is given by d3s dt3 If s = h 
1 - cos πθ 
2 β ∴ d3s = - π³ h sin 
πθ 
dt3 β³ 2 β Correct Option: D
The jerk is given by d3s dt3 If s = h 
1 - cos πθ 
2 β ∴ d3s = - π³ h sin 
πθ 
dt3 β³ 2 β
- In spur gears having involute teeth, the product of circular pitch and diametral pitch is _______.
-
View Hint View Answer Discuss in Forum
Pc × Pd = ∏
Correct Option: A
Pc × Pd = ∏

