81. A slider crank mechanism has slider mass of 10 kg, stroke of 0.2 m and rotates with a uniform angular velocity of 10 rad/s. The primary inertia forces of the slider are partially balanced by a revolving mass of 6 kg at the crank, placed at a distance equal to crank radius. Neglect the mass of connecting rod and crank. When the crank angle (with respect to slider axis) is 30°, the unbalanced force (in newton) normal to the slider axis is __________.

1. 1. 30

   
   
   

   2. 40

   
   
   

   3. 45

   
   
   

   4. 50

   
   
   

---

1. View Hint View Answer Discuss in Forum

   r =	0.2	= 0.1
   	2

   
   Now m= 6kg
   F = mr (10²) sin θ
   = 6 × 0.1 × 100 × sin 30° = 30 N

   Correct Option: A

   r =	0.2	= 0.1
   	2

   
   Now m= 6kg
   F = mr (10²) sin θ
   = 6 × 0.1 × 100 × sin 30° = 30 N

---

82. For a four bar linkage in toggle position, the value of mechanical advantage is

1. 1. 0.0

   
   
   

   2. 0.5

   
   
   

   3. 1.0

   
   
   

   4. ∞

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Mechanical advantages
   

   =	Load (output force)
   	Effort (input force)

   
   For a four bar linkage in toggle position, effort = 0
   ∴ Mechanical Advantage = ∞

   Correct Option: D

   Mechanical advantages
   

   =	Load (output force)
   	Effort (input force)

   
   For a four bar linkage in toggle position, effort = 0
   ∴ Mechanical Advantage = ∞

---

---

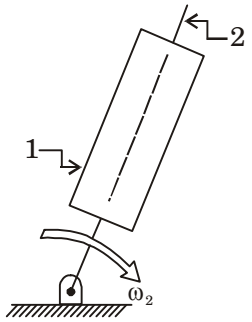
83. In the figure shown, the relative velocity of link 1 with respect of link 2 is 12 m/s. Link 2 rotates at a constant speed of 120 rpm. The magnitude of Coriolis component of acceleration of link 1 is
    

1. 1. 302 m/s²

   
   
   

   2. 906 m/s²

   
   
   

   3. 604 m/s²

   
   
   

   4. 1208 m/s²

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Velocity of link 1 with respect to link 2,
   V^{½ = 12 m/s}
   

   ω =	2πN	=	2π × 120	= 4π
   	60		60

   
   ∴ Corioli’s component of acceleration
   
   = 2V_½ω = 2 × 12 × 4π
   = 301.59 ≈ 302 m/s²

   Correct Option: A

   Velocity of link 1 with respect to link 2,
   V^{½ = 12 m/s}
   

   ω =	2πN	=	2π × 120	= 4π
   	60		60

   
   ∴ Corioli’s component of acceleration
   
   = 2V_½ω = 2 × 12 × 4π
   = 301.59 ≈ 302 m/s²

---

84. The circular disc shown in its plan view in the figure rotates in a plane parallel to the horizontal plane about the point O at a uniform angular velocity ω. Two other points A and B are located on the line OZ at distances r_A and r_B from O respectively.
    
    The acceleration of point B with respect to point A is a vector of magnitude

1. 1. 0

   
   
   

   2. ω (r_B– r_A) and direction same as the direction of motion of point B.

   
   
   

   3. ω (r_B – r_A) and direction opposite to be direction of motion of point B.

   
   
   

   4. ω ² (r_B – r_A) and direction being from Z to O.

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Acceleration of point B with respect to point A
   α_B/A = ω × υ_B/A
   = ω × ω (r_B - r_A)
   = ω² (r_B - r_A)
   and direction from Z to O.

   Correct Option: D

   Acceleration of point B with respect to point A
   α_B/A = ω × υ_B/A
   = ω × ω (r_B - r_A)
   = ω² (r_B - r_A)
   and direction from Z to O.

---

---

85. A four bar mechanism is shown in the figure. The link numbers are mentioned near the links. Input link 2 is rotating anticlockwise with a constant angular speed ω₂. Length of different links are
    O₂O₄ = O₂ A = L,
    AB = O₄ B = 2 L
    The magnitude of the angular speed of the output link 4 is ω₄ at the instant when link 2 makes an angle of 90° with O₂O₄ as shown. The ratio
    

    	ω4	is
    	ω2

    
    _____ (round off to two decimal places).
    

1. 1. 0.79

   
   
   

   2. 0.88

   
   
   

   3. 0.25

   
   
   

   4. 0.99

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   
   Now, O₄C = cos 75°
   O₄C = sin 75°
   ∆AO₂I₂₄ ≈ ∆BI₂₄C
   

   	L	=	√2Lsin75°
   	x		x + L + √2cos75°

   
   
   

   ⇒	L	= 0.2679
   	x

   
   

   	ω4	=	1	= 0.7887 ≈ 0.79
   	ω2		1 + 0.267

   Correct Option: A

   
   
   Now, O₄C = cos 75°
   O₄C = sin 75°
   ∆AO₂I₂₄ ≈ ∆BI₂₄C
   

   	L	=	√2Lsin75°
   	x		x + L + √2cos75°

   
   
   

   ⇒	L	= 0.2679
   	x

   
   

   	ω4	=	1	= 0.7887 ≈ 0.79
   	ω2		1 + 0.267

---