Communication miscellaneous Easy Questions and Answers | Page - 10

Communication miscellaneous

In an AM signal the received signal power is 10– 10 W with a maximum modulation signal of 5 kHz. The noise spectral density at the receiver input is 10^–18 W/Hz. If the noise power is restricted to the message signal bandwidth only, the signal-to-noise ratio at the input to the receiver is—

1. 43 dB
1. 66 dB
1. 56 dB
1. 33 dB

View Hint View Answer Discuss in Forum

Message signal BW f_m = 5kHz
Noise power density = 10^–18 W/Hz
Total noise power = 10^–18 × 5k = 5 × 10^–15W
Input signal-to-noise ratio
(SNR)_i= 10⁻¹⁸ = 2 × 10⁻⁴
5 ×10⁻¹⁵

or (SNR)_i = 10log₁₀ 2 × 10⁴ = 43dB
Hence alternative (A) is the correct choice.

Correct Option: A

Message signal BW f_m = 5kHz
Noise power density = 10^–18 W/Hz
Total noise power = 10^–18 × 5k = 5 × 10^–15W
Input signal-to-noise ratio
(SNR)_i= 10⁻¹⁸ = 2 × 10⁻⁴
5 ×10⁻¹⁵

or (SNR)_i = 10log₁₀ 2 × 10⁴ = 43dB
Hence alternative (A) is the correct choice.

Suppose we wish to transmit the signal x(t) = sin 200 πt + 2 sin 400πt using a modulation that create the signal g(t) = x (t) sin 400 πt. If the product g(t) sin 400 πt is passed through an ideal LPF with cut-off frequency 400π and pass band gain of 2, the signal obtained at the output of the LPF is—

1. sin 200 πt
1. 1 2 sin 200 πt
1. 2 sin 200 πt
1. 0

View Hint View Answer Discuss in Forum

Given that,
x(t) = sin 200πt + 2 sin 400πt
g(t) = x(t)·sin 400πt
or
g(t) = (sin 200πt + 2 sin 400πt) sin 400πt
If the product say
y(t) = g(t) sin 400 nt
y(t) = g(t)·sin 400πt
= (sin 200πt + 2 sin 400πt) sin² 400πt
= (sin 200πt + 2 sin 400πt) (1 − cos 800πt)
2

= 1 (sin 200πt) – sin (200πt) (cos 800πt) + sin (200πt) – sin (400πt) (cos 800πt)
2

= 1 sin (200πt) − 1 [sin (100πt) −sin (900πt)] + sin (400πt) − 1 [sin (1200πt) −sin (400πt)]
2 4 4

If this signal is passed through LPF with frequency 400π and gain 2, the output will be sin (200πt)
Hence alternative (A) is the correct choice.

Correct Option: A

Given that,
x(t) = sin 200πt + 2 sin 400πt
g(t) = x(t)·sin 400πt
or
g(t) = (sin 200πt + 2 sin 400πt) sin 400πt
If the product say
y(t) = g(t) sin 400 nt
y(t) = g(t)·sin 400πt
= (sin 200πt + 2 sin 400πt) sin² 400πt
= (sin 200πt + 2 sin 400πt) (1 − cos 800πt)
2

= 1 (sin 200πt) – sin (200πt) (cos 800πt) + sin (200πt) – sin (400πt) (cos 800πt)
2

= 1 sin (200πt) − 1 [sin (100πt) −sin (900πt)] + sin (400πt) − 1 [sin (1200πt) −sin (400πt)]
2 4 4

If this signal is passed through LPF with frequency 400π and gain 2, the output will be sin (200πt)
Hence alternative (A) is the correct choice.

Let x(t) be a signal band-limited to 1 kHz. Amplitude modulation is performed to produce signal g(t) = x(t) sin 2000 πt. A proposed demodulation technique is illustrated in fig. below. The ideal low pass filter has cut-off frequency 1 kHz and pass band gain 2. The y(t) would be—

1. 2 y(t)
1. y(t)
1. y(t) 2
1. 0

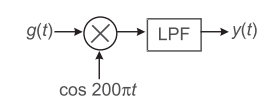
View Hint View Answer Discuss in Forum

Let the output of the modulator is S(t), So
S(t) = g(t)·cos 2000πt
or
S(t) = x(t)·sin 2000πt·cos 2000πt
or
S(t) = 1 x(t) sin 4000πt (˙.˙ 2 sin A cos A = sin2A)
2

or
S(jω) = 1 {[Xj(ω – 4000π)]} {[Xj (ω + 4000π)]} ...(A)
4j

Since given that x (t) is bandlimited to 1 kHz and from equation (A) we conclude that S (jω) is zero for |ω| ≤ 2000π because ω < 2πf_m = 2π 1000. When x₁(t) is passed through a LPF with cut-off frequency 2000π the output will be zero.
Hence alternative (D) is the correct choice.

Correct Option: D

Let the output of the modulator is S(t), So
S(t) = g(t)·cos 2000πt
or
S(t) = x(t)·sin 2000πt·cos 2000πt
or
S(t) = 1 x(t) sin 4000πt (˙.˙ 2 sin A cos A = sin2A)
2

or
S(jω) = 1 {[Xj(ω – 4000π)]} {[Xj (ω + 4000π)]} ...(A)
4j

Since given that x (t) is bandlimited to 1 kHz and from equation (A) we conclude that S (jω) is zero for |ω| ≤ 2000π because ω < 2πf_m = 2π 1000. When x₁(t) is passed through a LPF with cut-off frequency 2000π the output will be zero.
Hence alternative (D) is the correct choice.

10 signals, each band-limited to 5 kHz are to be transmitted over a single channel by frequency division multiplexing. If AM-SSB modulation guard band of 1kHz is used then the bandwidth of the multiplexed signal will be—

1. 79 kHz
1. 60 kHz
1. 59 kHz
1. 61 kHz

View Hint View Answer Discuss in Forum

The total signal bandwidth 5 × 10 = 50 kHz there will be 9 guard band between 10 signal, so guard bandwidth 9 kHz
Total bandwidth = 50 + 9 = 59 kHz.

Correct Option: C

The total signal bandwidth 5 × 10 = 50 kHz there will be 9 guard band between 10 signal, so guard bandwidth 9 kHz
Total bandwidth = 50 + 9 = 59 kHz.

In the circuit shown below between the terminal A and B an a.c. voltage source of frequency 400 Hz is connected. Another a.c. voltage of 1.0 MHz is connected between C and D. The output between E and F contains components at—

1. 400 Hz, 1MHz, 1000·4 kHz, 999·6 kHz
1. 1 MHz, 1000·4 kHz, 999·6 kHz
1. 400 Hz, 1000·4 kHz, 999·6 kHz
1. 1000·4 kHz, 999·6 kHz

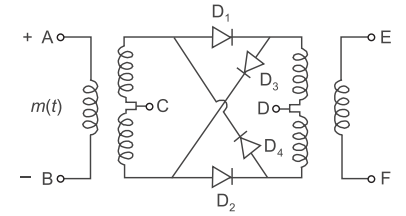
View Hint View Answer Discuss in Forum

The given circuit represents ring modulator. In ring modulator the output is proportional to the product of two i.e., m(t) and c(t) → DSB-SC signal
Here, m(t)=Am cos (2π × 400t)
= A_m (cos 2π × 0·4 × 10³t)
So the output s(t) = m(t )·c(t), contains components at frequency
f_c ± f_m
or (1000 ± 0·4) kHz or 1000·4 kHz and 999·6 kHz
Hence alternative (D) is the correct choice.

Correct Option: D

The given circuit represents ring modulator. In ring modulator the output is proportional to the product of two i.e., m(t) and c(t) → DSB-SC signal
Here, m(t)=Am cos (2π × 400t)
= A_m (cos 2π × 0·4 × 10³t)
So the output s(t) = m(t )·c(t), contains components at frequency
f_c ± f_m
or (1000 ± 0·4) kHz or 1000·4 kHz and 999·6 kHz
Hence alternative (D) is the correct choice.