Let x(t) be a signal band-limited to 1 kHz. Amplitude modulation

Home » Communication » Communication miscellaneous » Question

Let x(t) be a signal band-limited to 1 kHz. Amplitude modulation is performed to produce signal g(t) = x(t) sin 2000 πt. A proposed demodulation technique is illustrated in fig. below. The ideal low pass filter has cut-off frequency 1 kHz and pass band gain 2. The y(t) would be—

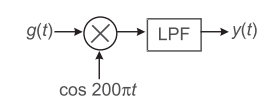
1. 2 y(t)
2. y(t)
3. y(t) 2
4. 0

Correct Option: D

Let the output of the modulator is S(t), So
S(t) = g(t)·cos 2000πt
or
S(t) = x(t)·sin 2000πt·cos 2000πt
or

S(t) =	1	x(t) sin 4000πt (˙.˙ 2 sin A cos A = sin2A)
	2

S(jω) =	1	{[Xj(ω – 4000π)]} {[Xj (ω + 4000π)]} ...(A)
	4j

Since given that x (t) is bandlimited to 1 kHz and from equation (A) we conclude that S (jω) is zero for |ω| ≤ 2000π because ω < 2πf_m = 2π 1000. When x₁(t) is passed through a LPF with cut-off frequency 2000π the output will be zero.
Hence alternative (D) is the correct choice.