31. A person distributes his pens among four friends A, B, C, D in the ratio
    

    =	1	:	1	:	1	:	1	What is the minimum number of pens
    	3		4		5		6

    that the person should have?

1. 1. 57

   
   
   

   2. 65

   
   
   

   3. 75

   
   
   

   4. 45

   
   
   

---

1. View Hint View Answer Discuss in Forum

   A : B : C
   

   =	1	:	1	:	1	:	1
   	3		4		5		6

   
   

   =	1	× 60 :	1	× 60 :	1	× 60 :	1	× 60
   	3		4		5		6

   
   [LCM of 3, 4, 5 & 6 = 60]
   = 20 : 15 : 12 : 10
   ∴  Minimum number of pens
   = 20 + 15 + 12 + 10 = 57

   Correct Option: A

   A : B : C
   

   =	1	:	1	:	1	:	1
   	3		4		5		6

   
   

   =	1	× 60 :	1	× 60 :	1	× 60 :	1	× 60
   	3		4		5		6

   
   [LCM of 3, 4, 5 & 6 = 60]
   = 20 : 15 : 12 : 10
   ∴  Minimum number of pens
   = 20 + 15 + 12 + 10 = 57

---

32. If x : y = 3 : 4 and y : z = 3 : 4,
    

    then	x + y + z	is equal to
    	3z

1. 1. 13

      27

   
   
   

   2. 1

      2

   
   
   

   3. 73

      84

   
   
   

   4. 37

      48

   
   
   

---

1. View Hint View Answer Discuss in Forum

   x : y = 3 : 4 = 9 : 12
   y : z = 3 : 4 = 12 : 16
   ∴  x : y : z = 9 : 12 : 16
   

   ∴	x + y + z	=	9k + 12k + 16k
   	3z		3 × 16k

   
   

   =	37
   	48

   Correct Option: D

   x : y = 3 : 4 = 9 : 12
   y : z = 3 : 4 = 12 : 16
   ∴  x : y : z = 9 : 12 : 16
   

   ∴	x + y + z	=	9k + 12k + 16k
   	3z		3 × 16k

   
   

   =	37
   	48

---

---

33. If A : B = 1 : 2, B : C = 3 : 4
    C : D = 6 : 9 and D : E = 12 : 16
    then A : B : C : D : E is equal to

1. 1. 1 : 3 : 6 : 12 : 16

   
   
   

   2. 2 : 4 : 6 : 9 : 16

   
   
   

   3. 3 : 4 : 8 : 12 : 16

   
   
   

   4. 3 : 6 : 8 : 12 : 16

   
   
   

---

1. View Hint View Answer Discuss in Forum

   A : B = 1 : 2 = 3 : 6
   B : C = 3 : 4 = 6 : 8
   C : D = 6 : 9 = 2 : 3 = 8 : 12
   D : E = 12 : 16
   ∴  A : B : C : D : E
   = 3 : 6 : 8 : 12 : 16

   Correct Option: D

   A : B = 1 : 2 = 3 : 6
   B : C = 3 : 4 = 6 : 8
   C : D = 6 : 9 = 2 : 3 = 8 : 12
   D : E = 12 : 16
   ∴  A : B : C : D : E
   = 3 : 6 : 8 : 12 : 16

---

34. In an alloy, the ratio of copper and zinc is 5 : 2. If 1.250 kg of zinc is mixed in 17 kg 500 g of
    alloy, then the ratio of copper and zinc will be

1. 1. 2 : 1

   
   
   

   2. 2 : 3

   
   
   

   3. 3 : 2

   
   
   

   4. 1 : 2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Weight of copper in 17kg 500 gm i.e. 17500 gm of alloy
   

   =	5	× 17500 = 12500 gm
   	7

   
   Weight of zinc = (17500 – 12500)
   = 5000 gm
   1250 gm of zinc is mixed in alloy.
   ∴  Total weight of zinc
   = 1250 + 5000 = 6250 gm.
   ∴  Required ratio
   = 12500 : 6250 = 2 : 1

   Correct Option: A

   Weight of copper in 17kg 500 gm i.e. 17500 gm of alloy
   

   =	5	× 17500 = 12500 gm
   	7

   
   Weight of zinc = (17500 – 12500)
   = 5000 gm
   1250 gm of zinc is mixed in alloy.
   ∴  Total weight of zinc
   = 1250 + 5000 = 6250 gm.
   ∴  Required ratio
   = 12500 : 6250 = 2 : 1

---

---

35. Alcohol and water in two vessels A and B are in the ratio 5 : 3 and 5 : 4 respectively. In what ratio, the liquids in both the vessels be mixed to obtain a new mixture in vessel C in the ratio 7 : 5 ?

1. 1. 2 : 3

   
   
   

   2. 3 : 2

   
   
   

   3. 3 : 5

   
   
   

   4. 2 : 5

   
   
   

---

1. View Hint View Answer Discuss in Forum

   By Alligation Rule
   
   

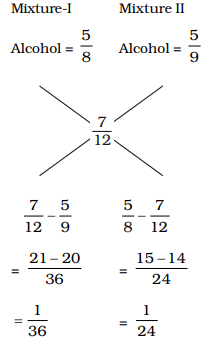
   ∴  Ratio =	1	:	1
   	36		24

   
   = 3 : 2

   Correct Option: B

   By Alligation Rule
   
   

   ∴  Ratio =	1	:	1
   	36		24

   
   = 3 : 2

---