276. 20 litres of a mixture contains 20% alcohol and the rest water. If 4 litres of water be mixed in it, the percentage of alcohol in the new mixture will be

1. 1. 33	1	%
      	3

   
   
   

   2. 16	2	%
      	3

   
   
   

   3. 25%

   
   
   

   4. 12	1	%
      	2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   In 20 litres of mixture,
   

   Alcohol ⇒	20 × 20	= 4 litres
   	100

   
   Water ⇒ 20 - 4 = 16 litres
   On adding 4 litres of water,
   Quantity of water ⇒ 16 + 4 = 20 litres
   Quantity of mixture = 24 litres
   

   ∴ Required percent =	4	× 100
   	24

   
   

   Correct Option: B

   In 20 litres of mixture,
   

   Alcohol ⇒	20 × 20	= 4 litres
   	100

   
   Water ⇒ 20 - 4 = 16 litres
   On adding 4 litres of water,
   Quantity of water ⇒ 16 + 4 = 20 litres
   Quantity of mixture = 24 litres
   

   ∴ Required percent =	4	× 100
   	24

   
   

   Required percent =	50	= 16	2	%
   	3		3

---

277. In what ratio must 25% of alcohol be mixed with 50% of alcohol to get a mixture of 40% strength alcohol ?

1. 1. 1 : 2

   
   
   

   2. 2 : 1

   
   
   

   3. 2 : 3

   
   
   

   4. 3 : 2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
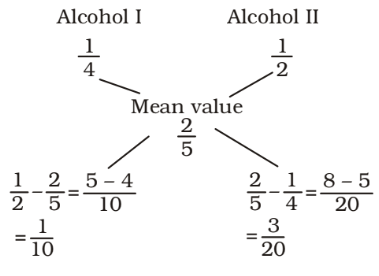
   ∴ Required ratio = Alcohol I : Alcohol II

   Correct Option: C

   
   ∴ Required ratio = Alcohol I : Alcohol II
   

   ∴ Required ratio =	1	:	3	= 2 : 3
   	10		20

---

---

278. In an alloy there is 12% of copper. To get 69 kg of copper, how much alloy will be required ?

1. 1. 424 kg

   
   
   

   2. 575 kg

   
   
   

   3. 828 kg

   
   
   

   4. 1736	2	kg
      	3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   ∵ 12 kg copper is contained in 100 kg of alloy
   69 kg copper is contained in
   

   ∴	100	× 69
   	12

   Correct Option: B

   ∵ 12 kg copper is contained in 100 kg of alloy
   69 kg copper is contained in
   

   ∴	100	× 69 = 575 kg of alloy
   	12

---

279. 15 litres of a mixture contains alcohol and water in the ratio 1 : 4. If 3 litres of Water is mixed in it, the percentage of alcohol in the new mixture will be

1. 1. 15%

   
   
   

   2. 16	2	%
      	3

   
   
   

   3. 17%

   
   
   

   4. 18	1	%
      	2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Alcohol = 15 ×	1	= 3 litres
   	5

   
   

   Water =15 ×	4	= 12 litres
   	5

   
   

   ∴ Required percentage =	3	× 100
   	15 + 3

   
   

   Correct Option: B

   Alcohol = 15 ×	1	= 3 litres
   	5

   
   

   Water =15 ×	4	= 12 litres
   	5

   
   

   ∴ Required percentage =	3	× 100
   	15 + 3

   
   

   Required percentage =	50	= 16	2	%
   	3		3

---

---

280. The ratio in which two sugar solutions of the concentrations 15% and 40% are to be mixed to get a solution of concentration 30% is

1. 1. 2 : 3

   
   
   

   2. 3 : 2

   
   
   

   3. 8 : 9

   
   
   

   4. 9 : 8

   
   
   

---

1. View Hint View Answer Discuss in Forum

   By mixture or alligation method , we have
   
   

   Correct Option: A

   By mixture or alligation method , we have
   
   ∴ Required ratio = 10 : 15 = 2 : 3

---