Number System
- The product of two fractions is 14/15 and their quotient is 35/24 The greater of the fractions is
-
View Hint View Answer Discuss in Forum
Let us assume the two fractions are p and q, where p > q
According to given question,∴ pq = 14 and p = 35 15 q 24
Solve this equation to get the answer.Correct Option: B
Let us assume the two fractions are p and q, where p > q
According to given question,∴ pq = 14 and p = 35 15 q 24
multiply both the given equation and we will get,∴ pq × p =
14 × 35 q 15 24 ⇒ p2 = 49 36 ⇒ p = 7 6
- In an examination, a student was asked to find 3/14 of a certain number, By mistake, he found 3/4 of it. His answer was 150 more than the correct answer. The given number is :
-
View Hint View Answer Discuss in Forum
Let us assume the number is p.
According to given question,3 p − 3 p = 150 4 14 ⇒ 21p − 6p = 150 28
Solve this equation further to get the answer.
Correct Option: B
Let us assume the number is p.
According to given question,3 p − 3 p = 150 4 14 ⇒ 21p − 6p = 150 28
⇒ 15p = 28 × 150⇒ p = 28 × 150 = 280 15
- A candidate in an examination was asked to find 5/14 of a certain number. By mistake he found 5/14 of it. Thus, his answer was 25 more than the correct answer. The number was :
-
View Hint View Answer Discuss in Forum
Let us assume the required number be n.
As per given question,⇒ n × 5 − n × 5 = 25 4 14
Solve this equation further to get the answer.Correct Option: A
Let us assume the required number be n.
As per given question,⇒ n × 5 − n × 5 = 25 4 14 ⇒ 5n 
1 − 1 
= 25 4 14 ⇒ 5n 
7 − 2 
= 25 ⇒ 5n × 5 = 25 28 28 ⇒ n = 25 × 28 = 28 5 × 5
- The least number that should be added to 2055, so that the sum is exactly divisible by 27 is
-
View Hint View Answer Discuss in Forum
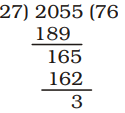
Correct Option: B
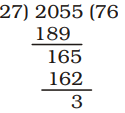
∴ Required number = 27 – 3 = 24
- If a and b are two odd positive integers, by which of the following integers is (a4 – b4) always divisible ?
-
View Hint View Answer Discuss in Forum
We know that , a4 – b4 = (a2)2 – (b2)2 = (a2 + b2) (a2 − b2) = (a2 + b2) (a + b) (a – b)
Correct Option: C
We know that , a4 – b4 = (a2)2 – (b2)2 = (a2 + b2) (a2 − b2) = (a2 + b2) (a + b) (a – b)
Let a = 3, b = 1
∴ Required number = ( 3 + 1 ) ( 3 – 1 ) = 4 x 2 = 8

