LCM and HCF
- The least perfect square, which is divisible by each of 21, 36 and 66 is
-
View Hint View Answer Discuss in Forum
LCM of 21, 36 and 66
∴ LCM = 3 × 2 × 7 × 6 × 11
⇒ LCM = 3 × 3 × 2 × 2 × 7 × 11
∴ Required number = 32 × 22 × 72 × 112Correct Option: C
LCM of 21, 36 and 66
∴ LCM = 3 × 2 × 7 × 6 × 11
⇒ LCM = 3 × 3 × 2 × 2 × 7 × 11
∴ Required number = 32 × 22 × 72 × 112
Required number = 213444
- Find the largest number of four digits such that on dividing by 15, 18, 21 and 24 the remainders are 11, 14, 17 and 20 respectively.
-
View Hint View Answer Discuss in Forum
As per the given details in question , we have
15 = 3 × 5
18 = 32 × 2
21 = 3 × 7
24 = 23 × 3
LCM of 15 , 18 , 21 and 24 = 8 × 9 × 5 × 7 = 2520
The largest number of four digits = 9999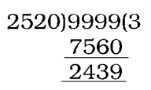
Correct Option: B
As per the given details in question , we have
15 = 3 × 5
18 = 32 × 2
21 = 3 × 7
24 = 23 × 3
LCM of 15 , 18 , 21 and 24 = 8 × 9 × 5 × 7 = 2520
The largest number of four digits = 9999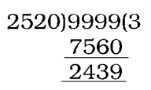
Required number = 9999 – 2439 – 4 = 7556
(Because 15 – 11 = 4
18 – 14 = 4
21 – 17 = 4
24 – 20 = 4)
- A, B, C start running at the same time and at the same point in the same direction in a circular stadium. A completes a round in 252 seconds, B in 308 seconds and C in 198 seconds. After what time will they meet again at the starting point ?
-
View Hint View Answer Discuss in Forum
Required time = LCM of 252, 308 and 198 seconds

∴ LCM = 2 × 2 × 7 × 9 × 11Correct Option: D
Required time = LCM of 252, 308 and 198 seconds

∴ LCM = 2 × 2 × 7 × 9 × 11
Required time = 2772 seconds
Required time = 46 minutes 12 seconds
- The least multiple of 13, which on dividing by 4, 5, 6, 7 and 8 leaves remainder 2 in each case is:
-
View Hint View Answer Discuss in Forum
According to question ,
LCM of 4, 5, 6, 7 and 8
LCM of 4, 5, 6, 7 and 8 = 2 × 2 × 2 × 3 × 5 × 7 = 840.
Let required number be 840K + 2 which is multiple of 13.
Least value of K for which ( 840K + 2 ) is divisible by 13 is K = 3Correct Option: C
According to question ,
LCM of 4, 5, 6, 7 and 8
LCM of 4, 5, 6, 7 and 8 = 2 × 2 × 2 × 3 × 5 × 7 = 840.
Let required number be 840K + 2 which is multiple of 13.
Least value of K for which ( 840K + 2 ) is divisible by 13 is K = 3
∴ Required number = 840 × 3 + 2
Required number = 2520 + 2 = 2522
- Find the greatest number of five digits which when divided by 3, 5, 8, 12 have 2 as remainder :
-
View Hint View Answer Discuss in Forum
Here , Remainder ( r ) = 2
As we know that When a number is divided by a, b , c or d leaving same remainder ‘r’ in each case then that number must be k + r where k is LCM of a, b , c and d.
The greatest number of five digits is 99999.
LCM of 3, 5, 8 and 12
∴ LCM = 2 × 2 × 3 × 5 × 2 = 120
After dividing 99999 by 120, we get 39 as remainder
99999 – 39 = 99960 = ( 833 × 120 )Correct Option: D
Here , Remainder ( r ) = 2
As we know that When a number is divided by a, b , c or d leaving same remainder ‘r’ in each case then that number must be k + r where k is LCM of a, b , c and d.
The greatest number of five digits is 99999.
LCM of 3, 5, 8 and 12
∴ LCM = 2 × 2 × 3 × 5 × 2 = 120
After dividing 99999 by 120, we get 39 as remainder
99999 – 39 = 99960 = ( 833 × 120 )
99960 is the greatest five digit number divisible by the given divisors.
In order to get 2 as remainder in each case we will simply add 2 to 99960.
∴ Greatest number = 99960 + 2 = 99962

