Control system miscellaneous Easy Questions and Answers | Page - 34

Control system miscellaneous

For a system with the transfer function H(s) = 3(s - 2) f, the matrix A
4s² - 2s + 1

in the state space form x = Ax + Bu is equal to

View Hint View Answer Discuss in Forum

It is state space representation using phase variable.
Standard form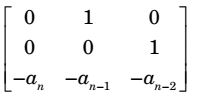
Thus ATQ a_n = 1, a_{n – 1} = – 2, a_{n – 2} = 4

Correct Option: B

It is state space representation using phase variable.
Standard form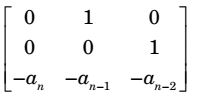
Thus ATQ a_n = 1, a_{n – 1} = – 2, a_{n – 2} = 4

A discrete real all pass system has a pole at z = 2 ∠ 30° : it, therefore

1. also has a pole at 1 ∠ 30°
  2
1. has a constant phase response over the zplane: arg | H(z)| = constant
1. is stable only, if it is anticausal
1. has a constant phase response over the unit circle: arg | H(e^jΩ)| = constant

View Hint View Answer Discuss in Forum

NA

Correct Option: D

NA

A closed-loop syst em has the char acterist ic function (s² – 4) (s + 1) + K (s – 1) = 0. Its root locus plot against K is

View Hint View Answer Discuss in Forum

NA

Correct Option: B

NA

The algebraic equation F(s) = s 5 – 3s 4 + 5s 3 – 7s 2 + 4s + 20 is given. F(s) = 0 has

1. a single complex root with the remaining roots being real
1. one positive real root and four complex roots, all with positive real parts
1. one negative real root, two imaginary roots, and two roots with positive real parts
1. one positive real root, two imaginary roots, and two roots with negative real parts

View Hint View Answer Discuss in Forum

F(s) = s ⁵ – 3s⁴ + 5s ³² – 7s ² + 4s + 20
We can solve it by making Routh Hurwitz array.
s ⁵ 1 5 4
s ⁴ – 3 – 7 20
s ³ 8/3 20/3 0
s ² 5 20 0
s ¹ 0 0 0
s ⁰ 20 0 0

We can replace 1st element of s 1 by 10.
If we observe 1st column, sign is changing two times, so we have two poles on right half side of imaginary axis and 5s² + 20 = 0.
So, s = ± 2 j and 1 pole on left side of imaginary axis.

Correct Option: C

F(s) = s ⁵ – 3s⁴ + 5s ³² – 7s ² + 4s + 20
We can solve it by making Routh Hurwitz array.
s ⁵ 1 5 4
s ⁴ – 3 – 7 20
s ³ 8/3 20/3 0
s ² 5 20 0
s ¹ 0 0 0
s ⁰ 20 0 0

We can replace 1st element of s 1 by 10.
If we observe 1st column, sign is changing two times, so we have two poles on right half side of imaginary axis and 5s² + 20 = 0.
So, s = ± 2 j and 1 pole on left side of imaginary axis.

Consider the following Nyquist plots of loop transfer functions over ω = 0 to ω = ∞ . Which of these plots represents a stable closed loop system?

1. (1) only
1. all, except (1)
1. all, except (3)
1. (1) and (2) only

View Hint View Answer Discuss in Forum

If GH plot incircles (– 1, j0) that is the critical point, then the system becomes unstable. So option 1 is there which does not enclose the (– 1, j0) other all are incircling the critical point.

Correct Option: A

If GH plot incircles (– 1, j0) that is the critical point, then the system becomes unstable. So option 1 is there which does not enclose the (– 1, j0) other all are incircling the critical point.