161. Consider the discrete-time system shown in the figure where the impulse response of G(z) is g(0) = 0, g(1) = g(2) = 1, g(3) = g(4) =... = 0.
     
     This system is stable for range of values of K

1. 1. 		-1 ,	1
      			2

   
   
   

   2. [-1 , 1]

   
   
   

   3. 	-	1	, 1
      		2

   
   
   

   4. 	-	1	, 2
      		2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   G(z) = z^{– 1} + z ^{– 2}
   Characteristic equation is
   1 + KG (z) = 0
   ⇒ 1 + K (z ^{– 1} + z ^{– 2}) = 0
   ⇒ z² + Kz + I = 0
   Using stability criteria,
   | K| < 1
   i.e. – 1 < K < 1
   

   Correct Option: B

   G(z) = z^{– 1} + z ^{– 2}
   Characteristic equation is
   1 + KG (z) = 0
   ⇒ 1 + K (z ^{– 1} + z ^{– 2}) = 0
   ⇒ z² + Kz + I = 0
   Using stability criteria,
   | K| < 1
   i.e. – 1 < K < 1
   

---

162. If the loop gain K of a negative feedback system having a loop transfer function
     

     	K(s + 3)
     	(s + 8)2

     
     is to be adjusted to induce a sustained oscillation then

1. 1. The frequency of this oscillation must be	4	rad / s
      	√3

   
   
   

   2. The frequency of this oscillation must be must be 4 rad/s

   
   
   

   3. The frequency of this oscillation must be must be 4 or	4	rad / s
      	√3

   
   
   

   4. such a K does not exist

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Characteristic equation is
   

   1 +	K(s + 3)	= 0
   	(s + 8)2

   
   ⇒ s² + (16 + K) s + 3K + 64 = 0
   Routh's array,
   
   ⇒ No such K exist to make all element of a row equal to 0.
   

   Correct Option: D

   Characteristic equation is
   

   1 +	K(s + 3)	= 0
   	(s + 8)2

   
   ⇒ s² + (16 + K) s + 3K + 64 = 0
   Routh's array,
   
   ⇒ No such K exist to make all element of a row equal to 0.
   

---

---

163. The system shown in the figure below
     
     can be reduced to the form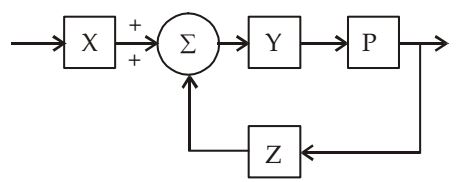
     
     with

1. 1. X = c0 s + c1 , Y =	1	, Z = b0s + b1
      	(s2 + a0s + a1)

   
   
   

   2. X = 1 , Y =	(c0s + c1)	, Z = b0s + b1
      	(s2 + a0s + a1)

   
   
   

   3. X = c1s + c0 , Y =	(b1s + b0)	, Z = 1
      	(s2 + a1s + a0)

   
   
   

   4. X = c1s + c0 , Y =	1	, Z = b1s + b0
      	(s2 + a1s + a0)

      
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   By block diagram, technique reduction method

   Correct Option: D

   By block diagram, technique reduction method

---

164. The transfer function of a linear time invariant system is given as
     

     G(s) =	1
     	s2 + 3s + 2

     
     The steady state value of the output of this system for a unit impulse input applied at time instant t = 1 will be
     

1. 1. 0

   
   
   

   2. 0.5

   
   
   

   3. 1

   
   
   

   4. 2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   ∴ G(s) =	y(s)	=	1
   	U(s)		s2 + 3s + 2

   
   

   ∴ y(s) =	1	U(s)
   	s2 + 3s + 2

   
   But U(t) = δ (t – 1)
   and U(s) = e^{– s}
   

   ∴ y(s) =	e– s
   	s2 + 3s + 2

   
   For steady state,
   

   =		e– s	=	1	= 0.5
   	s → 0	s2 + 3s + 2		2

   Correct Option: B

   ∴ G(s) =	y(s)	=	1
   	U(s)		s2 + 3s + 2

   
   

   ∴ y(s) =	1	U(s)
   	s2 + 3s + 2

   
   But U(t) = δ (t – 1)
   and U(s) = e^{– s}
   

   ∴ y(s) =	e– s
   	s2 + 3s + 2

   
   For steady state,
   

   =		e– s	=	1	= 0.5
   	s → 0	s2 + 3s + 2		2

---

---

165. Consider the feedback control system shown below which is subjected to a unit step input. The system is stable and has the following parameters k_p = 4, k_i = 10 , ω = 500 and ξ = 0.7
     
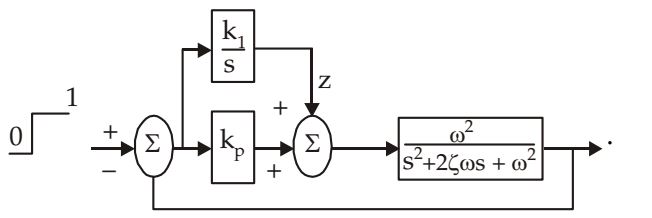
     The steady state value of z is

1. 1. 1
      

   
   
   

   2. 0.25

   
   
   

   3. 0.1

   
   
   

   4. 0

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Steady state value of z
   
   = 1

   Correct Option: A

   Steady state value of z
   
   = 1

---