Simplification
- The digit at unit’s place of the number (1570)2 + (1571)2 + (1572)2 + (1573)2 is :
-
View Hint View Answer Discuss in Forum
Unit’s digit in (1570)2 = 0
Unit’s digit in (1571)2 = 1
Unit’s digit in (1572)2 = 4
Unit’s digit in (1573)2 = 9
∴ Required unit’s digit
= Unit’s digit in (0 +1 + 4 + 9) = 4Correct Option: A
Unit’s digit in (1570)2 = 0
Unit’s digit in (1571)2 = 1
Unit’s digit in (1572)2 = 4
Unit’s digit in (1573)2 = 9
∴ Required unit’s digit
= Unit’s digit in (0 +1 + 4 + 9) = 4
- The digit at the unit’s place in the square-root of 15876 is :
-
View Hint View Answer Discuss in Forum
√15876 = 126
The digit at the unit’s place is 6.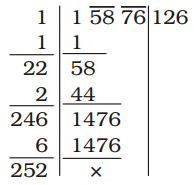
Correct Option: B
√15876 = 126
The digit at the unit’s place is 6.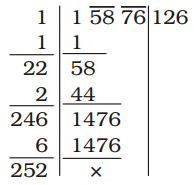
- The fourth root of 24010000 is
-
View Hint View Answer Discuss in Forum
√24010000 = 4900
Again, √4900 = 70
∴ 4√24010000 = 70Correct Option: D
√24010000 = 4900
Again, √4900 = 70
∴ 4√24010000 = 70
- Find the value of √156.25 + √0.0081 − √0.0361
-
View Hint View Answer Discuss in Forum
Expression
= √156.25 + √0.0081 − √0.0361
= 12.5 + 0.09 – 0.19 = 12.4Correct Option: C
Expression
= √156.25 + √0.0081 − √0.0361
= 12.5 + 0.09 – 0.19 = 12.4
- The square root of 33 – 4√35 is :
-
View Hint View Answer Discuss in Forum
33 – 4√35
= 33 – 2 × 2√5 × 7
= 33 – 2 × 2√7 × √5
= 28 + 5 – 2 × 2 √7 × √5
= (2√7)2 + (√5)2 – 2 × 2 √7 × √5
= (2√7 − √5)2
∴ √33 − 4√35
= √(2√7 − √5)2
= ±(2√7 − √5)Correct Option: D
33 – 4√35
= 33 – 2 × 2√5 × 7
= 33 – 2 × 2√7 × √5
= 28 + 5 – 2 × 2 √7 × √5
= (2√7)2 + (√5)2 – 2 × 2 √7 × √5
= (2√7 − √5)2
∴ √33 − 4√35
= √(2√7 − √5)2
= ±(2√7 − √5)

