Simplification
- What is the least number which should be subtracted from 0.000326, to have perfect square ?
-
View Hint View Answer Discuss in Forum
The given number has 6 decimal places.
Now,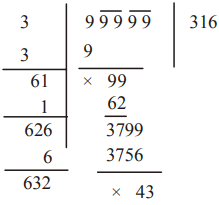
i.e. 326 – 2 = 324 Which is a perfect square of 18.
Therefore, 0.000002 should be subtracted from 0.000326 to make it a perfect square of 0.018.Correct Option: B
The given number has 6 decimal places.
Now,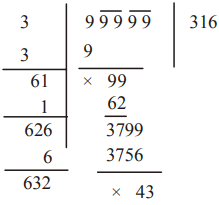
i.e. 326 – 2 = 324 Which is a perfect square of 18.
Therefore, 0.000002 should be subtracted from 0.000326 to make it a perfect square of 0.018.
- The least number that must be subtracted from 63520 to make the result a perfect square is :
-
View Hint View Answer Discuss in Forum
Obviously, 16 must be subtracted to make the result a perfect square.
i.e. 63520–16 = √63504 = 252Correct Option: A
Obviously, 16 must be subtracted to make the result a perfect square.
i.e. 63520–16 = √63504 = 252
- 1008 divided by which single digit number gives a perfect square?
-
View Hint View Answer Discuss in Forum
1008 = 4 × 4 × 3 × 3 × 7
∴ 1008 = (4 × 3)2 = (12)2 7 Correct Option: D
1008 = 4 × 4 × 3 × 3 × 7
∴ 1008 = (4 × 3)2 = (12)2 7
- The product of two numbers is 45 and their difference is 4. The sum of squares of the two numbers is
-
View Hint View Answer Discuss in Forum
Let the numbers be x and y and x > y.
∴ xy = 45
and x – y = 4
∴ x2 + y2 = (x – y)2 + 2xy
= (4)2 + 2 × 45 = 16 + 90
= 106Correct Option: D
Let the numbers be x and y and x > y.
∴ xy = 45
and x – y = 4
∴ x2 + y2 = (x – y)2 + 2xy
= (4)2 + 2 × 45 = 16 + 90
= 106
- The sum of a positive integer and its square is 2450. The positive integer is
-
View Hint View Answer Discuss in Forum
x2 + x = 2450
⇒ x (x +1) = 2450 = 49 × 50
∴ x = 49Correct Option: C
x2 + x = 2450
⇒ x (x +1) = 2450 = 49 × 50
∴ x = 49

