Surveying miscellaneous Easy Questions and Answers | Page - 7

Surveying miscellaneous

A levelling is carried out to establish the Reduced Levels (RL) of point R with respect to the Bench Mark (BM) at P. The staff readings taken are given below.

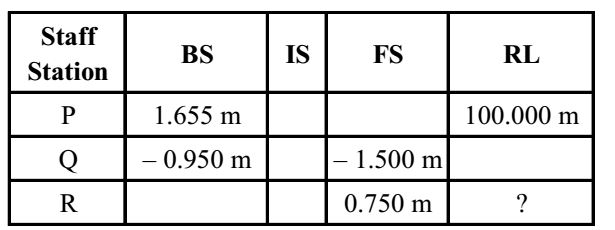
If RL of P is + 100.000 m, then RL (in m) of R is

1. 103.355
1. 103.155
1. 101.455
1. 100.355

View Hint View Answer Discuss in Forum

HI = RL + BS
RL = HI – FS
We find HI & RC from given values
Given RL at P is + 100 m.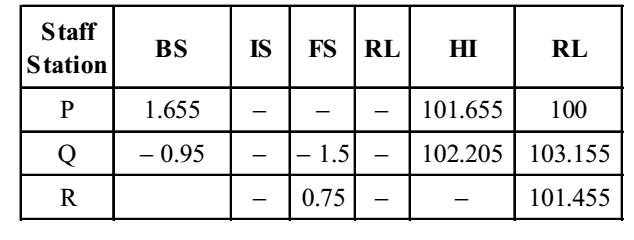

Correct Option: C

HI = RL + BS
RL = HI – FS
We find HI & RC from given values
Given RL at P is + 100 m.

The Reduced Levels (RLs) of the points P and Q are +49.600 m and +51.870 m respectively. Distance PQ is 20 m. The distance (in m from P) at which the +51.000 m contour cuts the line PQ is

1. 15.00
1. 12.33
1. 3.52
1. 2.27

View Hint View Answer Discuss in Forum

P and O are in same line at R. L = + 49.60 m
In ∆POQ,
sin θ = OQ = (51.870 - 49.6) = 0.1135
PQ 20

We have to find PS.
In ∆PSR
sin θ = SR = (51.0 - 49.6)
PS PS

0.1135 = 1.4
PS

∴ PS = 12.33 m

Correct Option: B

P and O are in same line at R. L = + 49.60 m
In ∆POQ,
sin θ = OQ = (51.870 - 49.6) = 0.1135
PQ 20

We have to find PS.
In ∆PSR
sin θ = SR = (51.0 - 49.6)
PS PS

0.1135 = 1.4
PS

∴ PS = 12.33 m

Two Pegs A and B were fixed on opposite banks of a 50 m wide river. The level was set up at A and the staff readings on Pegs A and B were observed as 1.350 m and 1.550 m, respectively. Thereafter the instrument was shifted and set up at B. The staff readings on Pegs B and A were observed as 0.750 m and 0.550 m, respectively. If the R.L. of Peg A is 100.200 m, the R.L. (in m) of Peg B is ______ .

1. 17
1. 40
1. 100
1. 85

View Hint View Answer Discuss in Forum

Thus is reciprocal levelling

∆h = (b₁ - a₁) + (b₂ - a₂)
2

∆h = (1.55 - 1.35) + (10.75 - 0.55) = 0.20
2

RL at B = RL at A – ∆h = 100.200 – 0.20 = 100

Correct Option: C

Thus is reciprocal levelling

∆h = (b₁ - a₁) + (b₂ - a₂)
2

∆h = (1.55 - 1.35) + (10.75 - 0.55) = 0.20
2

RL at B = RL at A – ∆h = 100.200 – 0.20 = 100

The latitude and departure of a line AB are +78 m and – 45.1 m, respectively. The whole circle bearing of the line AB is

1. 30°
1. 150°
1. 210°
1. 330°

View Hint View Answer Discuss in Forum

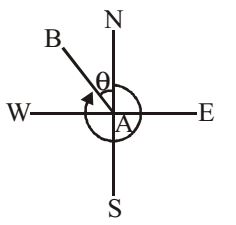
Since the latitude of line is positive and departure is negative, the line lies in the second quadrant.
∴ l cos θ = 78
l sin θ = – 45.1
⇒ tan θ = – 0.578
θ = – 30°
∴ WCB of AB = 360° – 30° = 330°

Correct Option: D

Since the latitude of line is positive and departure is negative, the line lies in the second quadrant.
∴ l cos θ = 78
l sin θ = – 45.1
⇒ tan θ = – 0.578
θ = – 30°
∴ WCB of AB = 360° – 30° = 330°

The horizontal distance between two stations P and Q is 100 m. The vertical angles from P and Q to the top of a vertical tower at T are 3° and 5° above horizontal, respectively. The vertical angles from P and Q to the base of the tower are 0.1° and 0.5° below horizontal, respectively. Stations P, and the tower are in the same vertical plane with P and Q being on the same side of T. Neglecting earth’s curvature and atmospheric refraction, the height (in m) of the tower is

1. 6.972
1. 12.387
1. 12.540
1. 128.745
1. None of the above

View Hint View Answer Discuss in Forum

None of the options is correct.
Let QC = x
In ∆AQC, h₁ = tan 5° .....(i)
x

In ∆APC, h₁ = tan 3° .....(ii)
x + 100

In ∆BQC, h₁ = tan 0.5° .....(iii)
x

In ∆BPC, h₁ = tan 1° .....(iv)
x + 100

Height of tower = h₁ + h₂
Solving (i) and (ii) we get, x = 149.39 m
Substituting in (i) We get, h₁ = 13.07 m
Substituting in (iii) we get, h₂ = 1.303 m
∴ height of h = h₁ + h₂ = 14.37 m

Correct Option: E

None of the options is correct.
Let QC = x
In ∆AQC, h₁ = tan 5° .....(i)
x

In ∆APC, h₁ = tan 3° .....(ii)
x + 100

In ∆BQC, h₁ = tan 0.5° .....(iii)
x

In ∆BPC, h₁ = tan 1° .....(iv)
x + 100

Height of tower = h₁ + h₂
Solving (i) and (ii) we get, x = 149.39 m
Substituting in (i) We get, h₁ = 13.07 m
Substituting in (iii) we get, h₂ = 1.303 m
∴ height of h = h₁ + h₂ = 14.37 m