Surveying miscellaneous

Surveying miscellaneous

Easy Questions

Surveying

Surveying miscellaneous
  1. The bearings of two inaccessible stations, S1 (Easting 500 m, Northing 500 m) and S2 (Easting 600 m, Northing 450 m) from a station S3 were observed as 225° and 153° 26' respectively. The independent Easting (in m) of station S3 is :








  1. View Hint View Answer Discuss in Forum


    Northing of S3 = 500 + L1 cos 45°
    = 450 + L2 cos 26° 34'
    ⇒ L1 cos 45° – L2 cos26° 34' = –50
    Easting of S3
    = 500 + L1 sin 45° = 600 – L2 sin 26° 34'
    L1 sin 45° + L2 sin 26°34' = 100
    ∴ L1 = 70.71, L2 = 111.80
    Easting of S3 = 500 + 70.71 × sin 45° ≈ 550m

    Correct Option: C


    Northing of S3 = 500 + L1 cos 45°
    = 450 + L2 cos 26° 34'
    ⇒ L1 cos 45° – L2 cos26° 34' = –50
    Easting of S3
    = 500 + L1 sin 45° = 600 – L2 sin 26° 34'
    L1 sin 45° + L2 sin 26°34' = 100
    ∴ L1 = 70.71, L2 = 111.80
    Easting of S3 = 500 + 70.71 × sin 45° ≈ 550m

  1. The combined correction due to curvature and refraction (in m) for a distance of 1 km on the surface of Earth is








  1. View Hint View Answer Discuss in Forum

    Combined correction due to curvature and refraction = 0.0673 d2
    = 0.0673 × (1)2 = 0.0673

    Correct Option: A

    Combined correction due to curvature and refraction = 0.0673 d2
    = 0.0673 × (1)2 = 0.0673

  1. In a region with magnetic declination of 2°E, the magnetic Fore bearing(FB) of a line AB was measured as N79°50'E. There was local attraction at A. To determine the correct magnetic bearing of the line, a point O was selected at which there was no local attraction. The magnetic FB of line AO and OA were observed to be S52°40'E and N50°20'W, respectively. What is the true FB of line AB?








  1. View Hint View Answer Discuss in Forum

    δ = 2° E
    Magnetic FB of AB = N 79° 50' E = 79° 50'
    Corrected FB of O A = N 50° 20' = 309°40'
    ∴ Correct BB of OA = 129° 40'
    Observed FB of AO = Observed BB of OA = 552°40' E = 127° 20'
    Error = MV – TV = – 2° 20'
    ∴ correction = 2°20'
    TB of FB of AB = N 79°50' E + δ + correction
    = N 79°50' E + 2 + 2°20'
    = N 84°10' E

    Correct Option: C

    δ = 2° E
    Magnetic FB of AB = N 79° 50' E = 79° 50'
    Corrected FB of O A = N 50° 20' = 309°40'
    ∴ Correct BB of OA = 129° 40'
    Observed FB of AO = Observed BB of OA = 552°40' E = 127° 20'
    Error = MV – TV = – 2° 20'
    ∴ correction = 2°20'
    TB of FB of AB = N 79°50' E + δ + correction
    = N 79°50' E + 2 + 2°20'
    = N 84°10' E

  1. In a closed loop traverse of 1 km total length, the closing errors in departure and latitude are 0.3 m and 0.4 m, respectively. The relative precision of this traverse will be :








  1. View Hint View Answer Discuss in Forum

    e = √l² + d²
    l = 0.3, d = 0.4
    ∴ e = √0.3² + 0.4² = √0.25 = 0.5 m

    Relative precision =
    0.5
    		 = 1 : 2000
    1000

    Correct Option: D

    e = √l² + d²
    l = 0.3, d = 0.4
    ∴ e = √0.3² + 0.4² = √0.25 = 0.5 m

    Relative precision =
    0.5
    		 = 1 : 2000
    1000

  1. The chainage of the intersection point of two straights is 1585.60 m and the angle of intersection is 140°. If the radius of a circular curve is 600.00 m, the tangent distance (in m) and length of the curve (in m). respectively are








  1. View Hint View Answer Discuss in Forum


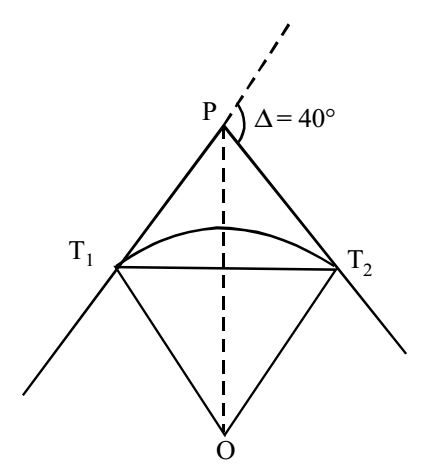
    ∆ = 180° – 140° = 40°

    Length of curve =
    πR ∆
    180°

    =
    π × 600 × 40
    		 = 418.82 m
    180

    Tangent distance, T = OT1 tan
    ∆
    		 (OT1 = radius = R)
    2

    = 600 × tan
    40
    		 = 218.88 m
    2

    Correct Option: C


    ∆ = 180° – 140° = 40°

    Length of curve =
    πR ∆
    180°

    =
    π × 600 × 40
    		 = 418.82 m
    180

    Tangent distance, T = OT1 tan
    ∆
    		 (OT1 = radius = R)
    2

    = 600 × tan
    40
    		 = 218.88 m
    2