Network theory miscellaneous

Network theory miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Network Theory

Network Elements and the Concept of Circuit
Network theory miscellaneous
  1. For the circuit shown below, the V1 = ?










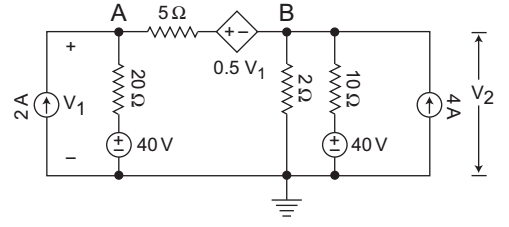
  1. View Hint View Answer Discuss in Forum

    The given circuit

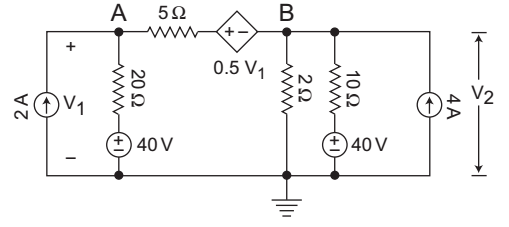
    Applying KCL at node A

    V1 - 20
    		 +
    V1 - 0.5V1 - V2
    		 = 2
    205

    or
    V1
    1
    		 +
    1
    		 -
    V2
    		 = 3
    20105

    or
    3V1
    		 -
    V2
    		 = 3
    205

    or
    3V1 – 4V2 = 60 . . . . . . …(i)
    KCL at node B
    V2 - V1 + 0.5V1
    		 +
    V2
    		 +
    V2 - 40
    		 = 4
    5210

    V2
    1
    		 +
    1
    		 +
    1
    		 -
    V1
    		 = 8
    521010

    or
    V2
    2 + 5 + 1
    		 -
    V1
    		 = 8
    108

    or
    8V1 – V1 = 80 …. . . (ii)
    From equation (i) and (ii)
    V1 = 40V and V2 = 15V
    Hence alternative (A) is the correct choice.

    Correct Option: A

    The given circuit

    Applying KCL at node A

    V1 - 20
    		 +
    V1 - 0.5V1 - V2
    		 = 2
    205

    or
    V1
    1
    		 +
    1
    		 -
    V2
    		 = 3
    20105

    or
    3V1
    		 -
    V2
    		 = 3
    205

    or
    3V1 – 4V2 = 60 . . . . . . …(i)
    KCL at node B
    V2 - V1 + 0.5V1
    		 +
    V2
    		 +
    V2 - 40
    		 = 4
    5210

    V2
    1
    		 +
    1
    		 +
    1
    		 -
    V1
    		 = 8
    521010

    or
    V2
    2 + 5 + 1
    		 -
    V1
    		 = 8
    108

    or
    8V1 – V1 = 80 …. . . (ii)
    From equation (i) and (ii)
    V1 = 40V and V2 = 15V
    Hence alternative (A) is the correct choice.

  1. For the circuit shown below, the Vout =?










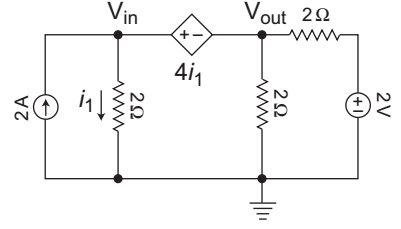
  1. View Hint View Answer Discuss in Forum

    The given circuit:

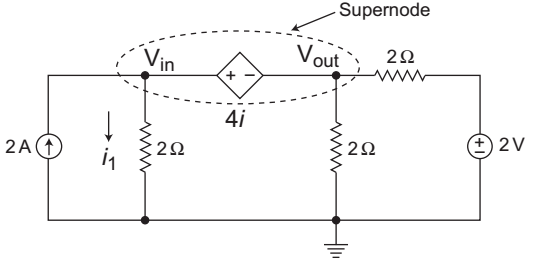
    Applying nodal equation for supernode

    Vin
    		 +
    Vout
    		 +
    Vout - 2
    		 = 2
    222

    or
    Vin + 2 Vout = 6 . . . . …(i)
    Again writting constraint equation for the dependent source inside the supernode. The dependent source voltage inside the supernode must satisfy.
    Vin – Vout = 4i1
    or
    Vin – Vout = 4 Vin/2
    or
    Vin + Vout = 0 . . . …(ii)
    From equation (i) and (ii) we get
    Vout = 6V.

    Correct Option: A

    The given circuit:

    Applying nodal equation for supernode

    Vin
    		 +
    Vout
    		 +
    Vout - 2
    		 = 2
    222

    or
    Vin + 2 Vout = 6 . . . . …(i)
    Again writting constraint equation for the dependent source inside the supernode. The dependent source voltage inside the supernode must satisfy.
    Vin – Vout = 4i1
    or
    Vin – Vout = 4 Vin/2
    or
    Vin + Vout = 0 . . . …(ii)
    From equation (i) and (ii) we get
    Vout = 6V.

  1. A linear resistive circuit has two inputs Vs1 and is2 with output Vout, as shown below. Table below shows the result of two sets of measurement taken in laboratory. Find the output voltage when the inputs are Vs1 = 10V and is2 = 8A.










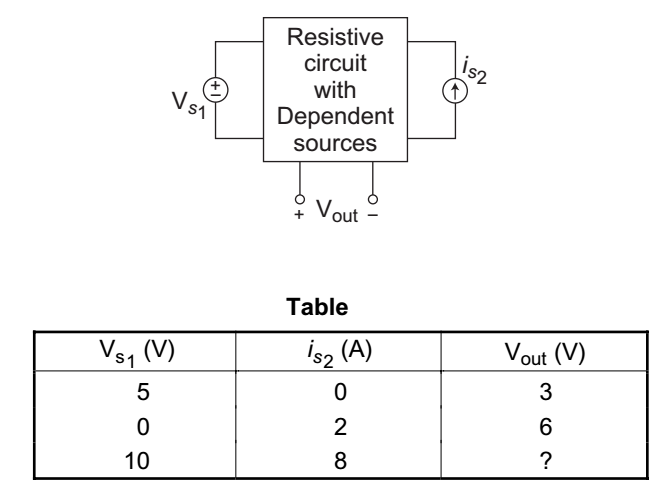
  1. View Hint View Answer Discuss in Forum

    From the linearity relation and from the given circuit

    Vout = AVs1 + Bis2 ⇒ (A) for appropriate A and B. The data from table imply that
    3 = A × 5 + B × 0, which gives A = 0·6
    Here A is dimensionless because Vout and Vs1 are both voltages.
    Also, 6 = A × 0 + B × 2, which gives B = 3Ω
    Here B has the unit of ohm. Therefore, the linear equation relating Vs1 and i s2 to Vout is
    Vout = 0·6Vs1 + 3is2
    Now, when Vs1 = 10V and is2 = 8A then
    Vout = 0·6 × 10 + 3 × 8 = 30V.

    Correct Option: A

    From the linearity relation and from the given circuit

    Vout = AVs1 + Bis2 ⇒ (A) for appropriate A and B. The data from table imply that
    3 = A × 5 + B × 0, which gives A = 0·6
    Here A is dimensionless because Vout and Vs1 are both voltages.
    Also, 6 = A × 0 + B × 2, which gives B = 3Ω
    Here B has the unit of ohm. Therefore, the linear equation relating Vs1 and i s2 to Vout is
    Vout = 0·6Vs1 + 3is2
    Now, when Vs1 = 10V and is2 = 8A then
    Vout = 0·6 × 10 + 3 × 8 = 30V.

  1. The average power delivered by the dependent current source for the circuit shown below—










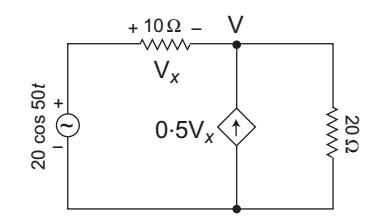
  1. View Hint View Answer Discuss in Forum

    The given circuit:

    From figure

    V – 20    0°
    		 +
    V
    		= 0·5Vx ......…(i)
    1020

    and V – 20 0° = – Vx
    or
    Vx = 20 0° – V …(ii)
    Now,
    V – 20    0°
    		 +
    V
    		= 0·5 [20 0° – V]
    1020

    or
    V
    1
    		 +
    1
    		 +
    1
    		= 2    0° + 10    0°
    10202

    or
    V = 18·46 0°
    and
    Vx = 20 0° – V = 20 0° – 18·46 0°
    = 1·54 0°
    Hence power delivered by the dependent source
    =
    V × 0·5Vx
    		 i.e.
    Vm Im
    		cos θ
    22

    =
    18·46 × 0·5 × 1·54
    2

    = 7·107W
    Hence alternative (D) is the correct choice.

    Correct Option: D

    The given circuit:

    From figure

    V – 20    0°
    		 +
    V
    		= 0·5Vx ......…(i)
    1020

    and V – 20 0° = – Vx
    or
    Vx = 20 0° – V …(ii)
    Now,
    V – 20    0°
    		 +
    V
    		= 0·5 [20 0° – V]
    1020

    or
    V
    1
    		 +
    1
    		 +
    1
    		= 2    0° + 10    0°
    10202

    or
    V = 18·46 0°
    and
    Vx = 20 0° – V = 20 0° – 18·46 0°
    = 1·54 0°
    Hence power delivered by the dependent source
    =
    V × 0·5Vx
    		 i.e.
    Vm Im
    		cos θ
    22

    =
    18·46 × 0·5 × 1·54
    2

    = 7·107W
    Hence alternative (D) is the correct choice.

  1. The impedance matrices of two, two-port networks are given by
    3
    2
    		and
    15
    5
    23525

    If these two networks are connected in series, the impedance matrix of the resulting two port network will be—








  1. View Hint View Answer Discuss in Forum

    The given matrices are:

    3
    2
    		 and
    15
    5
    23526

    When the two networks are connected in series the resulting impedance matrix is given by:
    3
    2
    		 +
    15
    5
    		 =
    18
    7
    23526728

    Correct Option: B

    The given matrices are:

    3
    2
    		 and
    15
    5
    23526

    When the two networks are connected in series the resulting impedance matrix is given by:
    3
    2
    		 +
    15
    5
    		 =
    18
    7
    23526728