1. I n the Maxwell bridge as shown in the figure below, the values of resistance R_x and inductance L_x of a coil are to be calculated after balancing the bridge. The component values are shown in the figure at balance. The values of R_x and L_x will respectively be
   
   

1. 1. 375 ohm. 75 mH

   
   
   

   2. 75 ohm, 150 mH

   
   
   

   3. 37.5 ohm, 75 mH

   
   
   

   4. 75 ohm, 75 mH

   
   
   

---

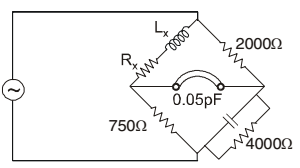
1. View Hint View Answer Discuss in Forum

   Applying the usual balance condition relation,
   Z₁ Z₄ = Z₂ Z₃.
   
   

   we have (R1 + jL1ω)	1/R4jC4ω	R2R3
   	R4 + 1/jC4ω

   
   

   or (R1 + jL1ω)	R4/jC4ω	R2R3
   	R4 + 1/jC4ω

   
   or R₁R₄ + jL₁ωR₄ = R₂R₃ + jR₂R₃R₄C₄ω
   

   ∴ R1 = R2	R3	L1 = R2R3C4
   	R4

   
   

   R1 = 2000 ×	750	= 375 ohm.
   	4000

   
   L_x = 2000 × 750 × 0.05 × 10-6 = 75 mH

   Correct Option: A

   Applying the usual balance condition relation,
   Z₁ Z₄ = Z₂ Z₃.
   
   

   we have (R1 + jL1ω)	1/R4jC4ω	R2R3
   	R4 + 1/jC4ω

   
   

   or (R1 + jL1ω)	R4/jC4ω	R2R3
   	R4 + 1/jC4ω

   
   or R₁R₄ + jL₁ωR₄ = R₂R₃ + jR₂R₃R₄C₄ω
   

   ∴ R1 = R2	R3	L1 = R2R3C4
   	R4

   
   

   R1 = 2000 ×	750	= 375 ohm.
   	4000

   
   L_x = 2000 × 750 × 0.05 × 10-6 = 75 mH

---

2. Dummy strain gauges are used for

1. 1. compensation of temperature changes

   
   
   

   2. increasing the sensitivity of bridge in which they are included

   
   
   

   3. compensating for different expansion

   
   
   

   4. calibration of strain gauges

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: A

   NA

---

---

3. Which of the following conditions are to be satisfied in the figure shown, so that the common variable shaft of resistance R₁ and R₂ can be graduated in frequency to measure the frequency of E under balanced condition?
   
   1. R₁ = R₃
   2. C₁ = C₃
   3. R₂ = 2R₄
   4. R₂ = R₄
   Select the correct answer using the codes given below:

1. 1. 1 and 4

   
   
   

   2. 1 and 2

   
   
   

   3. 2 and 4

   
   
   

   4. 1, 2 and 3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Writing the bridge balance equations:
   

   	R1 +	1		R4 = R2		R3(1/jC3ω)
   		jC1ω				R3 + (1/jC3ω)

   
   

   	R1 +	1		R4 = R2	R3
   		jC1ω			jR3C3ω + 1

   
   

   or		R1 +	1		(1 + jR3C3ω) =	R2R3
   			jC1ω			R4

   
   

   It gives; R1 + R3	C3	=	R2R3	,
   	C1		R4

   
   

   and R1 + R3C3ω =	1
   	C1ω

   
   

   or ω =	1
   	√R1R3C1C3

   
   If C₁ = C₃, then first equation becomes
   

   R1 + R3 =	R2R3
   	R4

   
   Again if R₁ = R₃ and the common variable short of resistance R₁ and R₂ can be graduated in frequency to measure the frequency ω. Thus conditions to be satisfied are
   C₁ = C₃, R₂ = 2R₄, and R₁ = R₃

   Correct Option: D

   Writing the bridge balance equations:
   

   	R1 +	1		R4 = R2		R3(1/jC3ω)
   		jC1ω				R3 + (1/jC3ω)

   
   

   	R1 +	1		R4 = R2	R3
   		jC1ω			jR3C3ω + 1

   
   

   or		R1 +	1		(1 + jR3C3ω) =	R2R3
   			jC1ω			R4

   
   

   It gives; R1 + R3	C3	=	R2R3	,
   	C1		R4

   
   

   and R1 + R3C3ω =	1
   	C1ω

   
   

   or ω =	1
   	√R1R3C1C3

   
   If C₁ = C₃, then first equation becomes
   

   R1 + R3 =	R2R3
   	R4

   
   Again if R₁ = R₃ and the common variable short of resistance R₁ and R₂ can be graduated in frequency to measure the frequency ω. Thus conditions to be satisfied are
   C₁ = C₃, R₂ = 2R₄, and R₁ = R₃

---

4. Piezoelectric accelerometers

1. 1. should not be used for high frequencies above 100 Hz

   
   
   

   2. should be used for low frequencies

   
   
   

   3. should use a monitoring source of low input impedance

   
   
   

   4. have a low natural frequency

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: B

   NA

---

---

5. The given figure shows wein bridge connection for frequency measurement. C and R are variables and ganged together. For balanced condition the expression for frequency is ƒ = 1/2πCR when
   

1. 1. R₁ = R₂

   
   
   

   2. R₁ = 2R₂

   
   
   

   3. R₁ = R₂/2

   
   
   

   4. R₁ = 3R₂

   
   
   

---

1. View Hint View Answer Discuss in Forum

   From the balance equation,
   

   R1		R +			= R2	R.	1
   			1				jωC
   			jωC			R +	1
   							jωC

   
   

   or	R1(jωCR + 1)	=	R2R
   	jωC		(jωCR + 1)

   
   or R₁ (– C²ω²R² + 1 + 2 jωCR) = jR₂CωR
   or 2CωRR₁ = CωRR₂
   

   ∴ R1 =	R2
   	2

   
   and – C²ω²R² + 1 = 0,
   

   or ω =	1
   	RC

   
   

   or ƒ =	1
   	2πRC

   Correct Option: C

   From the balance equation,
   

   R1		R +			= R2	R.	1
   			1				jωC
   			jωC			R +	1
   							jωC

   
   

   or	R1(jωCR + 1)	=	R2R
   	jωC		(jωCR + 1)

   
   or R₁ (– C²ω²R² + 1 + 2 jωCR) = jR₂CωR
   or 2CωRR₁ = CωRR₂
   

   ∴ R1 =	R2
   	2

   
   and – C²ω²R² + 1 = 0,
   

   or ω =	1
   	RC

   
   

   or ƒ =	1
   	2πRC

---