Control system miscellaneous
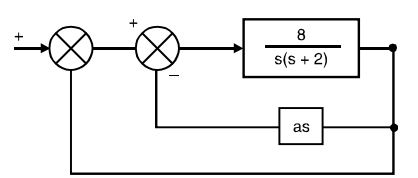
- The value of derivative feedback constant a, which will increase the damping ratio of the system to 0.7 is______
-
View Hint View Answer Discuss in Forum
Reduction of the block diagram
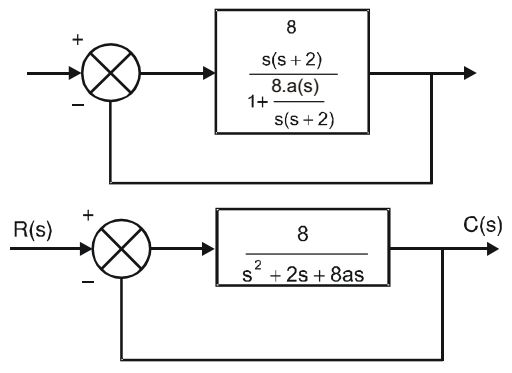
∴ C(s) = 8 = 8 s2 + (2 + 8a)s R(s) 1 + 8 s2 + (2 + 8a)s + 8 s2 + (2 + 8a)s
Characteristic equation is s2 + (2 + 8a) + 8 = 0
Equating with the equation
s2 + 2ξ ωn s + ωn 2 , we get
ωn = 2 √2
∴ ω(2 + 8a) = 2ξ ωn = 2 × 0.7 × 2 √2
⇒ a = 0.245Correct Option: C
Reduction of the block diagram

∴ C(s) = 8 = 8 s2 + (2 + 8a)s R(s) 1 + 8 s2 + (2 + 8a)s + 8 s2 + (2 + 8a)s
Characteristic equation is s2 + (2 + 8a) + 8 = 0
Equating with the equation
s2 + 2ξ ωn s + ωn 2 , we get
ωn = 2 √2
∴ ω(2 + 8a) = 2ξ ωn = 2 × 0.7 × 2 √2
⇒ a = 0.245
- For the signal– flow graph shown in the figure, which one of the following expressions is equal to the transfer function
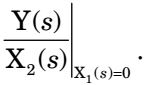

-
View Hint View Answer Discuss in Forum

when X1 (s) = 0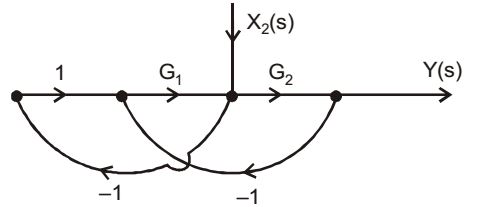
Forward path gain, P1 = G2
Loop gain, L1 = – G1
L2 = – G1 G2
∆ = 1 – (L1 + L2) + L1 L2
Transfer function,Y(s) = P1 ∆1 G2 (s) ∆ = G2 .1 | ∆1 = 1 1 + G1(1 + G2) 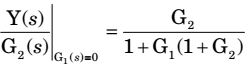
Correct Option: B

when X1 (s) = 0
Forward path gain, P1 = G2
Loop gain, L1 = – G1
L2 = – G1 G2
∆ = 1 – (L1 + L2) + L1 L2
Transfer function,Y(s) = P1 ∆1 G2 (s) ∆ = G2 .1 | ∆1 = 1 1 + G1(1 + G2) 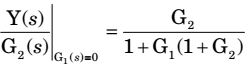
- For the transfer function
G(s) = 5(s + 4) s (s + 0.25)(s2 + 4s + 25)
The values of the constant gain term and the highest corner frequency of t he Bode plot respectively are
-
View Hint View Answer Discuss in Forum
G(s) = 5(s + 4) s(s + 0.25)(s2 + 4s + 25) G(jω) = 5(jω + 4) jω(jω + 0.25)[(jω)2 + 4jω + 25] = 5 × 4 × 4 
jω + 1 
4 jω(4jω + 1) 

jω 
2 + 4 jω + 1 

× 25 5 25 = 80 
jω + 1 
4 25 jω(4jω + 1) 

jω 
2 + 4(jω) + 1 

5 25 Constant gain term = 80 = 3.2 25
Corner frequencies are ω = 4, ω = 0.25, ω = 5
Then highest corner frequency ω = 5 rad/sec.Correct Option: A
G(s) = 5(s + 4) s(s + 0.25)(s2 + 4s + 25) G(jω) = 5(jω + 4) jω(jω + 0.25)[(jω)2 + 4jω + 25] = 5 × 4 × 4 
jω + 1 
4 jω(4jω + 1) 

jω 
2 + 4 jω + 1 

× 25 5 25 = 80 
jω + 1 
4 25 jω(4jω + 1) 

jω 
2 + 4(jω) + 1 

5 25 Constant gain term = 80 = 3.2 25
Corner frequencies are ω = 4, ω = 0.25, ω = 5
Then highest corner frequency ω = 5 rad/sec.
- Consider the system described by following state space equations

x1̇ 
= 
0 1 

x1 
+ 
0 
u ; y = [1 0] 
x1 
x2̇ -1 -1 x2 1 x2
If u is unit step input, then the steady state error of the system is
-
View Hint View Answer Discuss in Forum
Transfer function
⇒ C[SI - A]-1 .B. = [1 0] = 
S -1 
-1 
0 
1 (s + 1) 1 Transfer function = 1 s2 + s + 1 G(s) = 1 1 + G(s) s2 + s + 2 ⇒ G(s) = 1 s2 + s
Steady state error for unit stepess = A = 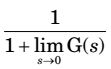
1 + Kp ess = 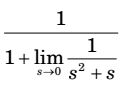
= 1 = 0 1 + ∞
Correct Option: A
Transfer function
⇒ C[SI - A]-1 .B. = [1 0] = 
S -1 
-1 
0 
1 (s + 1) 1 Transfer function = 1 s2 + s + 1 G(s) = 1 1 + G(s) s2 + s + 2 ⇒ G(s) = 1 s2 + s
Steady state error for unit stepess = A = 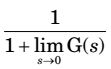
1 + Kp ess = 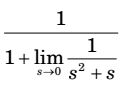
= 1 = 0 1 + ∞
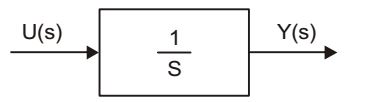
- Assuming zero initial condition, the response y(t) of the system given below to a unit step input u(t) is
-
View Hint View Answer Discuss in Forum

y(s) = 1 u(s) s y(s) = 1 × u(s) s
For unit step 1 / su(s) = 1 s y(s) = 1 s2
y(t) = t u(t)Correct Option: B

y(s) = 1 u(s) s y(s) = 1 × u(s) s
For unit step 1 / su(s) = 1 s y(s) = 1 s2
y(t) = t u(t)

