Sequences and Series
-
The next term of the sequence 1 , 3 1 , 6 , 8 3 ..............is : x - 2 4 4
-
View Hint View Answer Discuss in Forum
As per the given in question , we have
1 , 3 1 , 6 , 8 3 ........ 2 4 4
On adding 2.75 in each term of given sequence and we will get next term , As shown in figure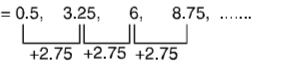
Correct Option: D
As per the given in question , we have
1 , 3 1 , 6 , 8 3 ........ 2 4 4
On adding 2.75 in each term of given sequence and we will get next term , As shown in figure
∴ Next term of the sequence = 8.75 + 2.75 = 11.5 = 11 1 2
- The odd one out from the sequence of numbers 19, 23, 29, 37, 43, 46, 47 is
-
View Hint View Answer Discuss in Forum
As per the given series in question ,
Except 46, all others are prime numbers.
46 = 2 × 23Correct Option: B
As per the given series in question ,
Except 46, all others are prime numbers.
46 = 2 × 23
Since , 46 is odd one out from the sequence of given numbers . So , option B is required answer .
- If the 10th term of the sequence a, a – b, a –2b, a – 3b, ... is 20 and the 20th term is 10, then the x th term of the series is
-
View Hint View Answer Discuss in Forum
Suppose a, a – b, a –2b ..... is an AP with first term = a and common difference = – b
Now, t10 = a + (10 – 1) × (–b)
⇒ 20 = a – 9b .... (i)
t20 = a + (20 – 1) × (–b)
⇒ 10 = a – 19 b ... (ii)
From equation (i) – (ii),
20 – 10 = a – 9b – a + 19 b
⇒ 10b = 10
⇒ b = 1Correct Option: D
Suppose a, a – b, a –2b ..... is an AP with first term = a and common difference = – b
Now, t10 = a + (10 – 1) × (–b)
⇒ 20 = a – 9b .... (i)
t20 = a + (20 – 1) × (–b)
⇒ 10 = a – 19 b ... (ii)
From equation (i) – (ii),
20 – 10 = a – 9b – a + 19 b
⇒ 10b = 10
⇒ b = 1
From equation (i) ,
20 = a – 9 ⇒ a = 29
∴ tx = 29 + (x – 1) × (–1 )
tx = 29 – x + 1 = 30 – x
- The seventh term of the sequence 1, 3, 6, 10, ......... is :
-
View Hint View Answer Discuss in Forum
The given series is based on the following pattern :

Correct Option: C
The given series is based on the following pattern :

Hence, the seventh term of the series will be 28.
- How many terms of the series “1 + 2 + 3 ......” add upto 5050?
-
View Hint View Answer Discuss in Forum
Let the number of terms be n.
∴ 1 + 2 + 3 + ..... + n = 5050⇒ n (n + 1) = 5050 2
⇒ n (n + 1) = 10100
Correct Option: C
Let the number of terms be n.
∴ 1 + 2 + 3 + ..... + n = 5050⇒ n (n + 1) = 5050 2
⇒ n (n + 1) = 10100
[or use splitting middle term method]
⇒ n (n + 1) = 100 × 101
⇒ n (n + 1) = 100 (100 + 1)
⇒ n = 100

