Let the four parts be (a - 3d), (a - d), (a + d) and (a + 3d).
(a - 3d) + (a - d) + (a +d ) + (a + 3d) = 124
⇒ a = 31
Also, (a -3d) (a + 3d) = (a - d) (a + d) - 128

Correct Option: B

Let the four parts be (a - 3d), (a - d), (a + d) and (a + 3d).
(a - 3d) + (a - d) + (a +d ) + (a + 3d) = 124
⇒ a = 31
Also, (a - 3d) (a + 3d) = (a - d) (a + d) - 128
⇒ a² - 9d² = a² - d² - 128
⇒ 8d² = 128
⇒ d = 4
a = 31, d = 4
So, the four parts are 19, 27, 35, 43.

Given that , 1² + 2² + 3² +......+ 10² = 385 ......( 1 )
∴ 2² + 4² + 6² + .... + 20² = 2² (1² + 2² + 3² + ..... + 10²)

Correct Option: B

Given that , 1² + 2² + 3² +......+ 10² = 385 ......( 1 )
∴ 2² + 4² + 6² + .... + 20² = 2² (1² + 2² + 3² + ..... + 10²)
2² + 4² + 6² + .... + 20² = 4 × 385 = 1540 { ∴ Using ( 1 ) }

The pattern is :
2 + 1³ = 2 + 1 = 3
3 + 2³ = 3 + 8 = 11
11 + 3³ = 11 + 27 = 38
38 + 4³ = 38 + 64 = 102
102 + 5³ = 102 + 125 = ?

Correct Option: B

The pattern is :
2 + 1³ = 2 + 1 = 3
3 + 2³ = 3 + 8 = 11
11 + 3³ = 11 + 27 = 38
38 + 4³ = 38 + 64 = 102
102 + 5³ = 102 + 125 = ?
∴ ? = 227
Thus , the next term in the sequence is 227 .

According to question,

∴ (1³ + 2³ + 3³ + ........ + 15³) – (1 + 2 + 3 + .... + 15) =		n(n + 1)		²	-		n(n + 1)
		2					2

Correct Option: A

According to question,

∴ (1³ + 2³ + 3³ + ........ + 15³) – (1 + 2 + 3 + .... + 15) =		n(n + 1)		²	-		n(n + 1)
		2					2

Required answer =		15 × 16		²	-		15 × 16
		2					2

According to question,
53, 48, 50, 50, 47, ....
The above series can be splitted into two series one in ascending order and other in descending order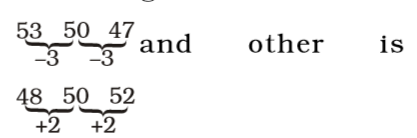

Correct Option: D

According to question,
53, 48, 50, 50, 47, ....
The above series can be splitted into two series one in ascending order and other in descending order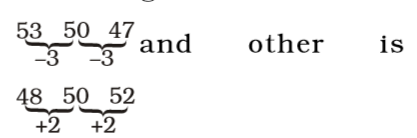

Hence, 52 will be the next number.