-
An inductor is connected in parallel with a capacitor as shown in the figure.
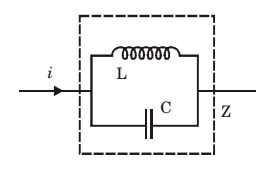
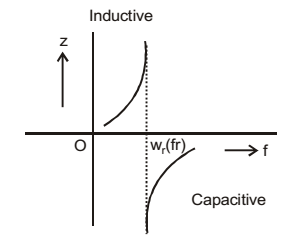
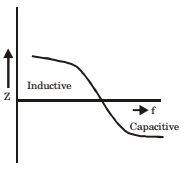
As the frequency of current i is increased, the impedance (Z) of the network varies as
Correct Option: B
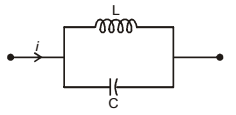
Since both the impedances are in parallel
| Z = | Ω | |
| (Z1 + Z2) |
where Z1 = jXL = jωLΩ
| Z2 = -jXc = | Ω | |
| ωc |
| Z = | (jωL) |  |  | = | |||
| ωc | C | ||||||
 | jωL - |  | j |  |  | ||
| ωc | ωc | ||||||
| Z = -j | ||
| (ω²LC - 1) |
| = -j | |||
| C | |||
 | ω² - |  | |
| LC | |||
Resonant frequency of the circuit
| ωr = | rad/sec | |
| √LC |
| Case (i): If ω < | ||
| √LC |
| Z = +j |  |  | Inductive | |
| (1/LC) - ω² |
| Case (ii): If ω > | ||
| √LC |
| Z = +j |  |  | Capacitive | |
| ω² - (1/LC) |
Note: It is infinite at Resonant frequency
Z = ∞ at
| ωr = | ||
| √LC |