6. The area of the triangle formed by the lines 5x + 7y = 35, 4x + 3y = 12 and x-axis is

1. 1. 160	sq.unit
      13

   
   
   

   2. 150	sq.unit
      13

   
   
   

   3. 140	sq.unit
      13

   
   
   

   4. 10 sq.unit

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given that :- 5x + 7y = 35... (i)
   4x + 3y = 12... (ii)
   By equation (i) × 4 – (ii) × 5
   On subtracting (20x + 28y = 140) - (20x + 15y = 60) ⇒ 13y = 80
   

   ⇒ y =	80	= Height of triangle
   	13

   
   Point of intersection on x-axis of equation
   5x + 7y = 35
   ⇒ 5x + 7 × 0 = 35
   ⇒ 5x = 35 ⇒ x = 7
   ∴ (7, 0)
   Similarly, point of intersection of
   4x + 3y = 12 = (3, 0)
   ∴ Base = 7 – 3 = 4
   

   Correct Option: A

   Given that :- 5x + 7y = 35... (i)
   4x + 3y = 12... (ii)
   By equation (i) × 4 – (ii) × 5
   On subtracting (20x + 28y = 140) - (20x + 15y = 60) ⇒ 13y = 80
   

   ⇒ y =	80	= Height of triangle
   	13

   
   Point of intersection on x-axis of equation
   5x + 7y = 35
   ⇒ 5x + 7 × 0 = 35
   ⇒ 5x = 35 ⇒ x = 7
   ∴ (7, 0)
   Similarly, point of intersection of
   4x + 3y = 12 = (3, 0)
   ∴ Base = 7 – 3 = 4
   

   ∴ Area =	1	× 4 ×	80	=	160	sq.unit
   	2		13		13

---

7. Minimum value of x2 +	1	- 3 is
   	x2 + 1

1. 1. - 3

   
   
   

   2. - 2

   
   
   

   3. 0

   
   
   

   4. - 1

   
   
   

---

1. View Hint View Answer Discuss in Forum

   As per the given question ,
   

   x2 +	1	- 3
   	x2 + 1

   
   is minimum when x = 0
   

   0 +	1	- 3
   	0 + 1

   Correct Option: B

   As per the given question ,
   

   x2 +	1	- 3
   	x2 + 1

   
   is minimum when x = 0
   

   0 +	1	- 3 = - 2
   	0 + 1

---

---

8. If x = a – b, y = b – c, z = c – a, then the numerical value of the algebraic expression x³ + y + z – 3xyz will be
   

1. 1. a + b + c

   
   
   

   2. 0

   
   
   

   3. 4 (a + b + c)

   
   
   

   4. 3 abc

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Here , x = a – b, y = b – c, z = c – a
   We have x + y + z = a – b + b – c + c – a = 0
   

   Correct Option: B

   Here , x = a – b, y = b – c, z = c – a
   We have x + y + z = a – b + b – c + c – a = 0
   ∴ x³ + y + z – 3xyz = 0
   Hence , the numerical value of algebraic expression is 0 .

---

9. The shaded region represents
   
   
   

1. 1. y ≤ x

   
   
   

   2. y ≥ – x

   
   
   

   3. y ≥ x

   
   
   

   4. y ≤ – x

   
   
   

---

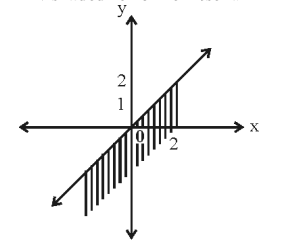
1. View Hint View Answer Discuss in Forum

   The shaded region represents
   y ≤ x

   Correct Option: A

   The shaded region represents
   y ≤ x

---

---

10. If 4x = 18y, then the value of		x	- 1		is
    		y

1. 1. 1

      3

   
   
   

   2. 7

      2

   
   
   

   3. 2

      3

   
   
   

   4. 3

      2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Here , 4x = 18y
   

   ⇒	x	=	18	=	9
   	y		4		2

   
   

   Correct Option: B

   Here , 4x = 18y
   

   ⇒	x	=	18	=	9
   	y		4		2

   
   

   ∴		x	- 1		=	9	- 1 =	7
   		y				2		2

---