Numerical Ability
- Students taking an exam are divided into two groups, P and Q such that each group has the same number of students. The performance of each of the students in a test was evaluated out of 200 marks. It was observed that the mean of group P was 105, while that of group Q was 85. The standard deviation of group P was 25, while that of group Q was 5. Assuming that the marks were distributed on a normal distribution, which of the following statements will have the highest probability of being TRUE?
-
View Hint View Answer Discuss in Forum
Group ‘P’
Mean (µ) = 105
Standard deviation (σ1) = 25
Pr (µ – σ ≤ x ≤ µ + σ) ≂ 0.6827
∴ 68% within one standard deviation
µ1 – σ1 = 105 – 25 = 80
µ1 + σ1 = 105 + 25 = 130
∴ range = 80 to 130
Distribution of P: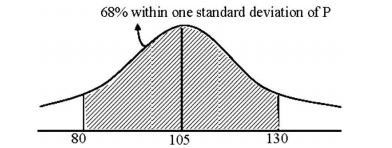
Group ‘Q’ Mean (µ2) = 85
Standard deviation (σ2) = 5
Pr (µ – σ ≤ x ≤ µ + σ) ≂ 0.6827
∴ 68% within one standard deviation
µ2 – σ2 = 85 – 5 = 80
µ2 + σ2 = 85 + 5 = 90
∴ Range of Q in one standard deviation is 80 to 90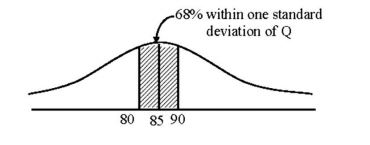
Distribution of ‘Q’ 68% wit hin one st andar d deviat ion of Q is narrower
∴ 68% within one standard deviation of Q means most students of group Q.
∴ Most students of group ‘Q’ scored marks in a narrower range than students in group ‘P’Correct Option: C
Group ‘P’
Mean (µ) = 105
Standard deviation (σ1) = 25
Pr (µ – σ ≤ x ≤ µ + σ) ≂ 0.6827
∴ 68% within one standard deviation
µ1 – σ1 = 105 – 25 = 80
µ1 + σ1 = 105 + 25 = 130
∴ range = 80 to 130
Distribution of P:
Group ‘Q’ Mean (µ2) = 85
Standard deviation (σ2) = 5
Pr (µ – σ ≤ x ≤ µ + σ) ≂ 0.6827
∴ 68% within one standard deviation
µ2 – σ2 = 85 – 5 = 80
µ2 + σ2 = 85 + 5 = 90
∴ Range of Q in one standard deviation is 80 to 90
Distribution of ‘Q’ 68% wit hin one st andar d deviat ion of Q is narrower
∴ 68% within one standard deviation of Q means most students of group Q.
∴ Most students of group ‘Q’ scored marks in a narrower range than students in group ‘P’
- P, Q, R and S are working on a project. Q can finish the task in 25 days, working alone for 12 hours a day. R can finish the task in 50 days, working alone for 12 hours per day. Q worked 12 hours a day but took sick leave in the beginning for two days, R worked 18 hours a day on all days. What is the ratio of work done by Q and R after 7 days from the start of the project?
-
View Hint View Answer Discuss in Forum
Q can finish the task = 25 days, 12 hrs/day = 300 hrs
⇒ 1 hr = 1 th 300
R can finish the task = 50 days, 12 hrs/day
= 50 × 12 = 600 hrs⇒ 1 hr = 1 th 600
Q working hours ⇒ (7 - 2) × 12 = 60hrs
R working hours 7 × 12 = 60hrs
After 7 days, the ratio of work done by Q and R
Correct Option: C
Q can finish the task = 25 days, 12 hrs/day = 300 hrs
⇒ 1 hr = 1 th 300
R can finish the task = 50 days, 12 hrs/day
= 50 × 12 = 600 hrs⇒ 1 hr = 1 th 600
Q working hours ⇒ (7 - 2) × 12 = 60hrs
R working hours 7 × 12 = 60hrs
After 7 days, the ratio of work done by Q and R
- If q–a = 1 /r and r–b = 1 /s and s–c = 1 /q of abc is. the value of abc is _______ .
-
View Hint View Answer Discuss in Forum
q-a = 1 ⇒ 1 = 1 ⇒ qa = r r qa r r-b = 1 ⇒ 1 = 1 ⇒ s = rb q rc s r-c = 1 ⇒ 1 = 1 ⇒ sc = q q sc q
qa=r⇒(sc)a =r⇒ sac = r
(sac)b=s⇒sabc=s¹
∴ abc = 1
∴ Option (c) is correctCorrect Option: C
q-a = 1 ⇒ 1 = 1 ⇒ qa = r r qa r r-b = 1 ⇒ 1 = 1 ⇒ s = rb q rc s r-c = 1 ⇒ 1 = 1 ⇒ sc = q q sc q
qa=r⇒(sc)a =r⇒ sac = r
(sac)b=s⇒sabc=s¹
∴ abc = 1
∴ Option (c) is correct
- In a huge pile of apples and oranges, both ripe and unripe mixed together, 15% are unripe fruits. Of the unripe fruits, 45% are apples. Of the ripe ones, 66% are oranges. If the pile contains a total of 5692000 fruits, how many of them are apples?
-
View Hint View Answer Discuss in Forum
Total no. of fruits = 5692000
Unripe type of apples = 45% of 15% of 5692000= 45 × 45 × 5692000 100 100
= 384210Ripe type of apples = 34 × 85 × 5692000 100 100
= 1644988
∴ Total number of apples = 384210 + 1644988 = 2029198Correct Option: A
Total no. of fruits = 5692000
Unripe type of apples = 45% of 15% of 5692000= 45 × 45 × 5692000 100 100
= 384210Ripe type of apples = 34 × 85 × 5692000 100 100
= 1644988
∴ Total number of apples = 384210 + 1644988 = 2029198
- In the given figure angle Q is a right angle, PS:QS = 3: 1, RT: QT = 5: 2 and PU: UR = 1 : 1. If area of triangle QTS is 20 cm, then the area of triangle PQR in cm2 is ________ .
-
View Hint View Answer Discuss in Forum
Let area of triangle PQR be ‘A’
SQ = 1 = 1 PQ 1 + 3 4 QT = 2 = 2 QR 2 + 5 7 Area of ∆le QTS = 1 × SQ × QT 2 = 1 × 
1 PQ 
× 
2 QR 
2 4 7 = = 1 × 1 × 
1 × PQ × QR 
4 7 2 = 14 × Area of ∆le PQR 14
Given20cm² = 1 × A 14
∴ A = 14 × 20 = 280 cm²Correct Option: D
Let area of triangle PQR be ‘A’
SQ = 1 = 1 PQ 1 + 3 4 QT = 2 = 2 QR 2 + 5 7 Area of ∆le QTS = 1 × SQ × QT 2 = 1 × 
1 PQ 
× 
2 QR 
2 4 7 = = 1 × 1 × 
1 × PQ × QR 
4 7 2 = 14 × Area of ∆le PQR 14
Given20cm² = 1 × A 14
∴ A = 14 × 20 = 280 cm²

