Engineering Mechanics Miscellaneous
- A bullet of mass m travels at a very high velocity V (as shown in the figure) and gets embedded inside the block of mass M initially at rest on a rough horizontal floor. The block with the bullet is seen to move a distance 's' along the floor. Assuming μ to be the coefficient of kinetic friction between the block and the floor and g the acceleration due to gravity. What is the velocity V of the bullet?
-
View Hint View Answer Discuss in Forum
Let, m = mass of the bullet
v = velocity of bullet
M = mass of the block
u = final velocity of system (block + bullet)
From conservation of linear momentum
mv = (M + m)u⇒ u = mv m + M
For horizontal equilibrium of body (M + m)g = N
Fr = Frictional force = μN = u(M + m)gFrictional retardation = μ(M + m)g = -μg (M + m) 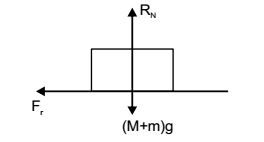
(–ve sign shows that acceleration is opposite to motion)
Let vf = final velocity of system = 0
v²f = u² + 2as
u² + 2as = 0
u² – 2μgs = 0
From equation (i)
mv 
² = 2μgs M + m mv = √2μgs M + m ⇒ v = M + m √2μgs m Correct Option: A
Let, m = mass of the bullet
v = velocity of bullet
M = mass of the block
u = final velocity of system (block + bullet)
From conservation of linear momentum
mv = (M + m)u⇒ u = mv m + M
For horizontal equilibrium of body (M + m)g = N
Fr = Frictional force = μN = u(M + m)gFrictional retardation = μ(M + m)g = -μg (M + m) 
(–ve sign shows that acceleration is opposite to motion)
Let vf = final velocity of system = 0
v²f = u² + 2as
u² + 2as = 0
u² – 2μgs = 0
From equation (i)
mv 
² = 2μgs M + m mv = √2μgs M + m ⇒ v = M + m √2μgs m
- A ball A of mass m falls under gravity from a height h and strikes another ball B of mass m which is supported at rest on a spring of stiffness k. Assume perfect elastic impact. Immediately after the impact
-
View Hint View Answer Discuss in Forum
In a perfectly elastic collision between equal masses of two bodies, velocities exchange on impact.
Velocity just before impect = Velocity immediately after impact.
Correct Option: B
In a perfectly elastic collision between equal masses of two bodies, velocities exchange on impact.
Velocity just before impect = Velocity immediately after impact.
- A force of 100 N is applied to the centre of a circular disc, of mass 10 kg and radius 1 m, resting on a floor as shown in the figure. If the disc rolls without slipping on the floor, the linear acceleration (in m/s²) of the centre of the disc is _________ (correct to two decimal places).

-
View Hint View Answer Discuss in Forum

m = 10 kg, r = 1 m
100 – f = maCM = mr∝ ...(A) '
[Tarque]CM = ICM’∝f × r = mr² × ∝ 2
2f = mr∝
2f = macmf = m × acm ...........(ii) 2
By (A) & (B) we get100 - macm = macm 2
we get on solvingaCM = 6.67 m s² Correct Option: B

m = 10 kg, r = 1 m
100 – f = maCM = mr∝ ...(A) '
[Tarque]CM = ICM’∝f × r = mr² × ∝ 2
2f = mr∝
2f = macmf = m × acm ...........(ii) 2
By (A) & (B) we get100 - macm = macm 2
we get on solvingaCM = 6.67 m s²

