-
A bullet of mass m travels at a very high velocity V (as shown in the figure) and gets embedded inside the block of mass M initially at rest on a rough horizontal floor. The block with the bullet is seen to move a distance 's' along the floor. Assuming μ to be the coefficient of kinetic friction between the block and the floor and g the acceleration due to gravity. What is the velocity V of the bullet?
-
-
M + m √2μgs m -
M - m √2μgs m -
μ(M + m) √2μgs mm -
M √2μgs m
-
Correct Option: A
Let, m = mass of the bullet
v = velocity of bullet
M = mass of the block
u = final velocity of system (block + bullet) 
From conservation of linear momentum
mv = (M + m)u
| ⇒ u = | ||
| m + M |
For horizontal equilibrium of body (M + m)g = N
Fr = Frictional force = μN = u(M + m)g
| Frictional retardation = | = -μg | |
| (M + m) |
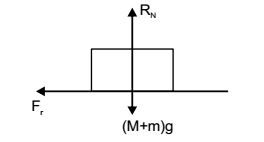
(–ve sign shows that acceleration is opposite to motion)
Let vf = final velocity of system = 0
v²f = u² + 2as
u² + 2as = 0
u² – 2μgs = 0
From equation (i)
 |  | ² | = 2μgs | |
| M + m |
| = √2μgs | |
| M + m |
| ⇒ v = | √2μgs | |
| m |

