Boats and Streams
- A man can row 6 km/h in still water. If the speed of the current is 2 km/h, it takes 3 hours more in upstream than in the downstream for the same distance. The distance is
-
View Hint View Answer Discuss in Forum
Let the required distance be d km.
∴ d - d = 3 6 - 2 6 + 2 ⇒ d - d = 3 4 8 ⇒ 2d - d = 3 8
⇒ d = 3 × 8 = 24 km.
Second method to solve this question :
Here, Speed of Boat = 6 km/hr
Speed of Current = 2 km/hr
t1 = 3 + t2Speed of Boat = t1 + t2 Speed of Stream t1 - t2
Correct Option: B
Let the required distance be d km.
∴ d - d = 3 6 - 2 6 + 2 ⇒ d - d = 3 4 8 ⇒ 2d - d = 3 8
⇒ d = 3 × 8 = 24 km.
Second method to solve this question :
Here, Speed of Boat = 6 km/hr
Speed of Current = 2 km/hr
t1 = 3 + t2Speed of Boat = t1 + t2 Speed of Stream t1 - t2 6 = 3 + 2t2 2 3
⇒ 9 = 3 + 2t2
⇒ t2 = 3 hrs
Distance = Speed × time
Hence , Distance = (6 + 2) × 3 = 24 km
- Speed of motorboat in still water is 45kmph. If the motorboat travels 80 km along the stream in 1 hour 20 minutes, then the time taken by it to cover the same distance against the stream will be
-
View Hint View Answer Discuss in Forum
Let the speed of the current be p kmph
Speed of motorboat in still water = 45kmph
∴ Rate downstream = (p + 45) kmph.
According to the question,80 = 1 hour 20 minutes = 4 hours p + 45 3
⇒ 4p + 180 = 240
⇒ 4p = 240 – 180 = 60⇒ p = 60 kmph = 15 kmph 4
Rate upstream = 45 – 15 = 30 kmph
Correct Option: C
Let the speed of the current be p kmph
Speed of motorboat in still water = 45kmph
∴ Rate downstream = (p + 45) kmph.
According to the question,80 = 1 hour 20 minutes = 4 hours p + 45 3
⇒ 4p + 180 = 240
⇒ 4p = 240 – 180 = 60⇒ p = 60 kmph = 15 kmph 4
Rate upstream = 45 – 15 = 30 kmph∴ Required time = 80 hours 30 Required time = 8 = 2 hour 40 minutes 3
- Speed of a boat is 5 km per hour in still water and the speed of the stream is 3 km per hour. If the boat takes 3 hours to go to a place and come back, the distance of the place is :
-
View Hint View Answer Discuss in Forum
Here , Speed of a boat in still water = 5 km per hour and the speed of the stream = 3 km per hour.
Let the required distance be d km, thend + d = 3 5 + 3 5 - 3 d + d = 3 8 2 ⇒ d + 4d = 3 8
⇒ 5 d = 24⇒ d = 24 = 4.8 km 5
Using the given formula :
Here, p = 5, q = 3, t = 3d = t(p² - q²) 2p
Correct Option: C
Here , Speed of a boat in still water = 5 km per hour and the speed of the stream = 3 km per hour.
Let the required distance be d km, thend + d = 3 5 + 3 5 - 3 d + d = 3 8 2 ⇒ d + 4d = 3 8
⇒ 5 d = 24⇒ d = 24 = 4.8 km 5
Using the given formula :
Here, p = 5, q = 3, t = 3d = t(p² - q²) 2p d = 3(5² - 3²) = 3 × 16 = 4.8 km 2 × 5 10
- The speed of a boat along the stream is 12 km/h and against the stream is 8 km/h. The time taken by the boat to sail 24 km in still water is
-
View Hint View Answer Discuss in Forum
Let the speed of boat in still water be x kmph and that of current be y kmph., then
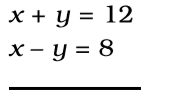
⇒ 2x = 20
⇒ x = 10 kmph.
∴ speed of boat in still water be 10 kmph.
Distance = 24 km∴ Required time = 24 = 2.4 hours 10
We can find the required answer with the help of given formula :
Here, p = 12, q = 8Speed of Boat = 
p + q 
2
Correct Option: C
Let the speed of boat in still water be x kmph and that of current be y kmph., then
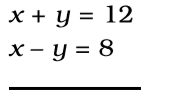
⇒ 2x = 20
⇒ x = 10 kmph.
∴ speed of boat in still water be 10 kmph.
Distance = 24 km∴ Required time = 24 = 2.4 hours 10
We can find the required answer with the help of given formula :
Here, p = 12, q = 8Speed of Boat = 
p + q 
2 Speed of Boat = 
12 + 8 
= 10km/hr 2 Time taken = Distance Speed Time taken = 24 = 2.4 hrs. 10
- On a river, Q is the mid-point between two points P and R on the same bank of the river. A boat can go from P to Q and back in 12 hours, and from P to R in 16 hours 40 minutes. How long would it take to go from R to P ?
-
View Hint View Answer Discuss in Forum
Let PQ = QR = d km.
Let speed of boat in still water be p kmph. and speed of current be q kmph.
According to the question,d + d = 12 ..........(i) p + q p - q and 2d = 16 40 p - q 60 ⇒ 2d = 16 2 = 50 ......(ii) p - q 3 3
By equation (i) × 2 – (ii),⇒ 2d + 2d - 2d = 24 - 50 p + q p - q p - q 3
Correct Option: D
Let PQ = QR = d km.
Let speed of boat in still water be p kmph. and speed of current be q kmph.
According to the question,d + d = 12 ..........(i) p + q p - q and 2d = 16 40 p - q 60 ⇒ 2d = 16 2 = 50 ......(ii) p - q 3 3
By equation (i) × 2 – (ii),⇒ 2d + 2d - 2d = 24 - 50 p + q p - q p - q 3 ⇒ 2d = 72 - 50 = 22 = 7 1 hours p + q 3 3 3

