-
A circular rod of diameter d and length 3d is subjected to a compressive force F acting at the top point as shown below. Calculate the stress at the bottom most support point A
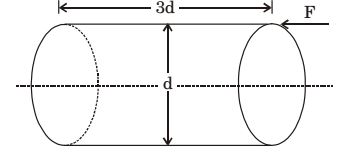
-
-
12F πd2
-
16F πd2
-
- 4F πd2
-
- 12F πd2
-
Correct Option: A

Stress due to Axial force
| σa = | = | = | (compressive) | |||
| A | (π / 4)d2 | πd2 |
Stress due to bending:
| σb = | = | × | = | (tensile) | ||||
| 2 | 2 | |||||||
| I | d4 | πd2 | ||||||
| 64 | ||||||||
Combined stress:
σr = σa + σb
| σr = | + | = | ||||
| πd2 | πd2 | πd2 |
| σr = | ||
| πd2 |

