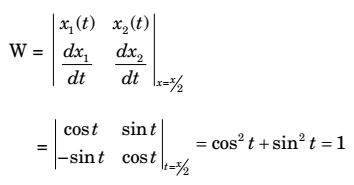-
Consider two solutions x(t) = x1 (t) and x(t) = x2 (t) of the differential equation
d²x(t) + x(t) = 0, t > 0, dx
such that x2 =dx2(t) |t=0 = 1. dt 
-
- 1
- –1
- 0
- π/2
Correct Option: A
Given Differential equation is
| + x(t) = 0 | ||
| dt² |
Auxiliary equation is m² + 1 = 0
m = 0 ± i
Complementary y solution is
xc = c1 cost + c² sin t
Particular solution xp = 0
∴ General solution x = c1 cos t + c2 sin t
Let x1 (t) = cos t x2 (t) = sin t
| learly x1 (0) = 1 | = 0 and x2 (0) = 0, | = 1 | ||
| dt | dt |