-
Two poles of equal height are standing opposite to each other on either side of a road which is 100 m wide. From a point between them on road, angle of elevation of their tops are 30° and 60°. The height of each pole (in metre) is
-
- 25 √3
- 20 √3
- 28 √3
- 30 √3
Correct Option: A
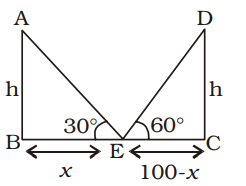
AB = CD = h metre (Height of pole)
From ∆ABE,
| tan 30° = | x |
| ⇒ | = | ⇒ √3h = x .........(i) | ||
| √3 | x |
From ∆DEC,
| tan 60° = | 100 - x |
| ⇒ √3 = | 100 - x |
⇒ √3 ( 100 - x) = h
⇒ √3 (100 - √3h) = h
[From equation (i)]
⇒ 100 √3 - 3h ⇒ 4h = 100√3
⇒ h = 25 √3 metre

