-
The angle of elevation of an aeroplane from a point A on the ground is 60°. After a straight flight of the plane for 30 seconds, the angle of elevation becomes 30°. If the palne flies at a constant height of 3600√3 metre, what is the speed of plane?
-
- 864 kmph
- 846 kmph
- 684 kmph
- None of these
- 864 kmph
Correct Option: A
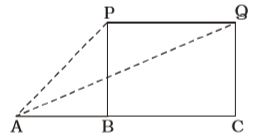
P and Q = Positions of plane
∠PAB = 60°, ∠QAB = 30°, PB = 3600√3 metre
In ∆ABP,
| tan 60° = | ||
| AB |
| ⇒ √3 = | ||
| AB |
⇒ AB = 3600 metre
In ∆ACQ,
| tan 30° = | ||
| AC |
| ⇒ | = | ||
| √3 | AC |
⇒ AC = 3600 × 3 = 10800 metre
∴ PQ = BC = AC – AB = 10800 – 3600 = 7200 metre
This distance is covered in 30 seconds.
| ∴ Speed of plane = | = 240 m/sec. | |
| 30 |
| = |  | 240 × |  | |
| 5 |
= 864 kmph

