-
From an aeroplane just over a river, the angle of depression of two palm trees on the opposite bank of the river are found to be 60° and 30° respectively. If the breadth of the river is 400 metres, then the height of the aeroplane above the river at that instant is (Assume √3 = 1.732)
-
- 173.2 metres
- 346.4 metres
- 519.6 metres
- 692.8 metres
Correct Option: A
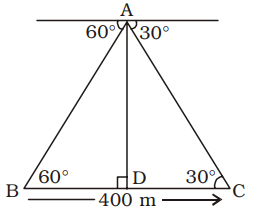
BC = River = 400 metre
AD = Height of plane = h metre
BD = x metre (let)
∴ CD = (400 – x) metre
From ∆ABD
| tan 60° = | BD |
| ⇒√ 3 = | x |
⇒ h = √3 x metre
| ⇒x = | metre ...(i) | √3 |
From ∆ACD,
| tan 30° = | CD |
| ⇒ | = | √3 | 400 - x |
⇒ √3h = 400 – x
| ⇒√3h = 400 - | √3 |
[From equation (i)]
| ⇒√3h + | = 400 | √3 |
| ⇒ | = 400 | √3 |
⇒ 4h = 400 √3
| ⇒ h = | 4 |
= 100 √3 metre
= 100 × 1.732 = 173.2 metre

