-
In the figure, BD and CD are angle bisectors of ∠ ABC and ∠ ACE, respectively. Then ∠ BDC is equal to :
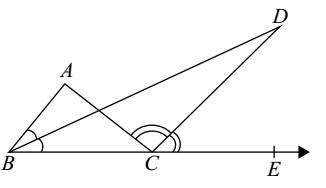
-
- ∠BAC
- 2∠BAC
-
1 ∠BAC 2 -
1 ∠BAC 3 - None of these
Correct Option: C
From above given figure , we have
In ΔABC, ∠ACE = ∠ABC + ∠BAC
Similarly in ΔBCD, ∠BDC = ∠DCE − ∠DBC [Ext. angle prop. of a Δ]
| But ∠DCE = | 1 | ∠ACE and |
| 2 |
| ⇒ | 1 | ∠DBC = | 1 | ∠ABC |
| 2 | 2 |
Now ∠BDC = ∠DCE - ∠DBC
| = | 1 | (∠ACE - ∠ABC) |
| 2 |
| = | 1 | (∠ACE + ∠ABC - ∠ACE) |
| 2 |
| ∴ ∠BDC = | 1 | ∠BAC |
| 2 |

