Database miscellaneous

Database miscellaneous

Easy Questions
Moderate Questions

Database

Database miscellaneous
  1. Let R1 (A, B, C) and R2 (D, E) be two relational sachemas, where the primary keys are shown underlined, and let C be a foreign key in R1 referring to R2. Suppose there is no violation of the above referential integrity constraint in the corresponding relational instances r1 and r2 .Which one of the following relational algebra expressions would necessarily produce an empty relation?








  1. View Hint View Answer Discuss in Forum

    C is an attribute in R1 but D is a key in K2.
    So consider ΠC (r1) – ΠD (r2)
    So the result of this query would be all those tuples

    which are in ΠC (r1) but not in ΠD (r2). Since D is a key so it has all the possible values of C. So difference would always be empty. Hence (b) is correct.

    Correct Option: B

    C is an attribute in R1 but D is a key in K2.
    So consider ΠC (r1) – ΠD (r2)
    So the result of this query would be all those tuples

    which are in ΠC (r1) but not in ΠD (r2). Since D is a key so it has all the possible values of C. So difference would always be empty. Hence (b) is correct.

  1. Let r be a rational instance with schema R = (A, B, C, D). We define r1 = ΠA, B, C(r) and r2 = ΠA, D(r). Let s = r1 * r2 where * denotes natural join. Given that the decomposition of r into r1 and r2 is lossy, which one of the following is true?








  1. View Hint View Answer Discuss in Forum

    R = (A, B, C, D)
    r1 = ΠA , B , C (R) and r2 = ΠA , D (r)
    s = r1 * r2
    The tuples in s are more than that of r. Also, s consists of all the tuples of r along with other tuples. Therefore, the most appropriate relation is r ⊂ s .

    Correct Option: C

    R = (A, B, C, D)
    r1 = ΠA , B , C (R) and r2 = ΠA , D (r)
    s = r1 * r2
    The tuples in s are more than that of r. Also, s consists of all the tuples of r along with other tuples. Therefore, the most appropriate relation is r ⊂ s .

  1. Consider the relation enrolled (student, course) in which (student, course) is the primary key, and the relation paid (student, amount) where student is the primary key. Assume no null values and no foreign keys or integrity constraints. Assume that amount 6000, 7000, 8000, 9000 and 10000 were each paid by 20% of the students. Consider these query plans (Plan1 on left, Plan2 on right) to “list all courses taken by students who have paid more than x”:

    A disk seek takes 4 ms, disk data transfer bandwidth is 300 MB/s and checking a tuple to see if amount is greater than x takes 10 µs. Which of the following statements is correct?








  1. View Hint View Answer Discuss in Forum

    Given that left hand side is plan1 and right hand side is plan2 .
    Plan1
    1. select records form paid
    2. joins them
    Plan2
    1. joins records from paid
    2. records are checked
    The seek time of disk is 4 ms and data transfer rate is 300 MB/s.
    So, if x = 5000. Although the output remains the same but the plan1 executes faster than plan2 for all databases.

    Correct Option: C

    Given that left hand side is plan1 and right hand side is plan2 .
    Plan1
    1. select records form paid
    2. joins them
    Plan2
    1. joins records from paid
    2. records are checked
    The seek time of disk is 4 ms and data transfer rate is 300 MB/s.
    So, if x = 5000. Although the output remains the same but the plan1 executes faster than plan2 for all databases.

  1. Consider the relation employee (name, sex, supervisorName) with name as the key. supervisorName gives the name of the supervisor of the employee under consideration. What does the following tuple relational calculus query produce?
    {e.name | employee (e) ∧}
    (∀ x) [ ̚ employee (x) ∨ x. supervisor Name ≠ e. name vx. sex = “male”]








  1. View Hint View Answer Discuss in Forum

    We are given with the below relational calculus:
    {e.name|employee (e) ∧}
    (∀x)[ ̚ employee (x) ∨ x.x.supervisorName ≠ x.sex = “male” ]}
    {e.name|employee (e) ∧} gives he name of the employee
    (∀x)[ ̚ employee (x)j v x.supervisorName ≠ x.sex = “male” ]} tells that employee does not have nay female subordinate.

    Correct Option: C

    We are given with the below relational calculus:
    {e.name|employee (e) ∧}
    (∀x)[ ̚ employee (x) ∨ x.x.supervisorName ≠ x.sex = “male” ]}
    {e.name|employee (e) ∧} gives he name of the employee
    (∀x)[ ̚ employee (x)j v x.supervisorName ≠ x.sex = “male” ]} tells that employee does not have nay female subordinate.

  1. Given an instance of the STUDENTS relation as shown below :

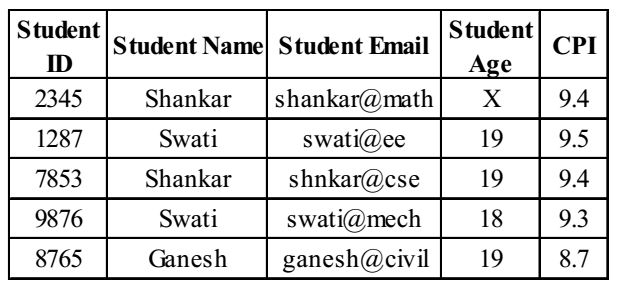
    For (StudentName, StudentAge) to be a key for this instance, the value X should NOT be equal to _____________ .








  1. View Hint View Answer Discuss in Forum

    Age cannot be 19 as (Student Name, Student Age) is a key.

    Correct Option: A

    Age cannot be 19 as (Student Name, Student Age) is a key.