-
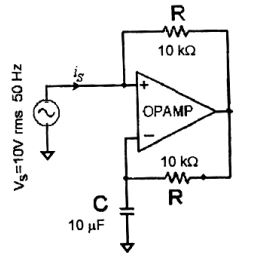
The following circuit has R = 10k&ohm:, C = 10&m;F. The input voltage is a sinusoid at 50Hz with an rms value of 10V under ideal conditions, the current is from the source is
-
- 10 π mA leading by 90°
- 20 π mA leading by 90°
- 10 mA leading by 90°
- 10 π mA lagging by 90°
Correct Option: D
| Xc = | = | = | ohm | |||
| ω C | 2π × 50 × 10μF | π |
| VA = | . V0 | |
| -jXc + R |
| ∴ V0 = | . VA | |
| -jXc |
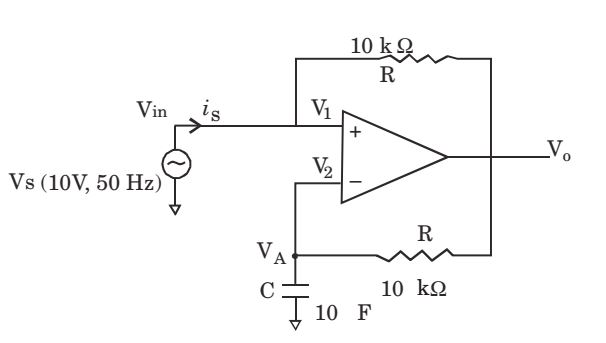
Assuming virtual ground,
Vin = VA = 10V
| ∴ V0 = | . 10 | |
| -jXc |
| Current , is = | ||
| R |
| = |  | 10 - | .10 |  | ||
| 104 | -jXc |
| = |  | 1 - |  | |||
| 103 | -jXc |
| = |  |  | ||||
| 103 | -jXc |
| = | = | . | × | ||||||
| 103 | jXc | j | 103 | (103 / π) |
| = | = (10π mA) ∠ -90° lagging | |
| j |
Alternately
V1 = Vs = R . is + V0
| V2 = Vo | |||
| jωC | = Vo | ||
| + R | 1 + jωRC | ||
| jωC | |||
| But Vo = A(V1 – V2) = A |  | Vs - |  | ||
| 1 + jωRC |
| ⇒ Vo |  | 1 + |  | = AVs | |
| 1 + jωRC |
| ⇒ | = | ≃ 1 + jωRC | ||
| Vs | 1 + jωRC + A |
= 1 + j 100 π × 104 × 10 × 10–6 = 1 + j 10π
⇒ Vo = Vs (1 + j 10π) = 10 (1 + j 10π)
But Vs = R . is + Vo
| or is = | = | |||
| R | 10 × 103 |
= – j 10π mA = 10π ∠– 90° mA

