The characteristic equation of a closed-loop system is s(s

The characteristic equation of a closed-loop system is s(s + 1)(s + 3) + k(s + 2) = 0, k > 0. Which of the following statements is true?

1. Its roots are always real
2. It cannot have a breakaway point in the range – 1 < Re[s] < 0
3. Two of its roots tend to infinity along the asymptotes Re[s] = – 1
4. It may have complex roots in the right half plane

Given : s(s + 1) (s + 3) + k(s + 2) = 0; k > 0

⇒ 1 +	k(s + 2)	= 0
	s(s + 1)(s + 3)

But 1 + G(s) H(s) = 0

∴ G(s) H(s ) =	k(s + 2)
	s(s + 1)(s + 3)

Roots s = 0, s = – 1, s = – 3 (poles); s = – 2 (zero)
It has real pole or zeros.

φ_A =	2q + 1	× 180°
	n - m

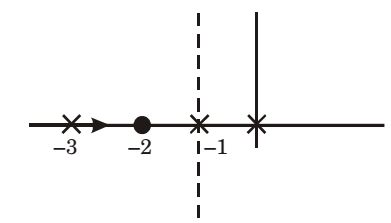
At s = 0, Asymptotes

φ₀ =	(2*0 + 1)180	= 90°
	2

At s = 1, φ₁ =	(2*1 + 1)180	= 270°
	2

Centroid,

(-σ_A) =	∑ real parts of poles - ∑ real poles of zeros
	number of poles - number of zeros

∴ Re[s] = – 1