-
A 400 V, 50 Hz, 4 pole, 1400 rpm, star connected squirrel cage induction motor has the following parameters referred to the stator
Rr' = 1.0 Ω , Xs = Xr' = 1.5 Ω
Neglect stator resistance and core and rotational losses of the motor.
The motor is controlled from a 3-phase voltage source inverter with constant V/f control. The stator line-to-line voltage (rms) and frequency to obtain the maximum torque at starting will be
-
- 20.6 V, 2.7 Hz
- 133.3 V, 16.7 Hz
- 266.6 V, 33.3 Hz
- 323.3 V, 40.3 Hz
Correct Option: B
For maximum torque, slip,
| sm = | (Neglecting stator resistance) | |
| Xsm + X'rm |
For starting torque, sm = 1
Xsm + X 'rm = Rr ' (∴ R'r = 1 Ω)
∴ 2π fm Ls 2π fm + Lr ' = 1
| ⇒ fm = | ||
| 2π(Ls + Lr) |
where, m indicates value of reactance corresponding to maximum torque frequency and fm is frequency at maximum torque.
| But Ls = | = | ||
| 2π × 50 | 2π × 50 |
| and L'r = | ||
| 2π × 50 |
Putting values of Ls and L'r, we get
| fm = | = | = 16.7 Hz | |||||
| + | 3 | ||||||
| 50 | 50 | ||||||
| For constant | , | |
| f |
| = | = 8 | |||
| f1 | 50 |
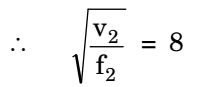
⇒ v2 = f2 × 8 = 16.7 × 8 = 133.3 volts
Hence answer is (133.3V, 16.7 Hz).

