A ball of mass 3 kg moving with a velocity of 4 m/s undergoes

Home » Engineering Mechanics » Engineering Mechanics Miscellaneous » Question

A ball of mass 3 kg moving with a velocity of 4 m/s undergoes a perfectly-elastic directcentral impact with a stationary ball of mass m. After the impact is over, the kinetic energy of the 3 kg ball is 6 J. The possible value(s) of m is/are

1. 1 kg, 6 kg
2. 1 kg, 9 kg
3. 6 kg only
4. 1 kg only

Correct Option: B

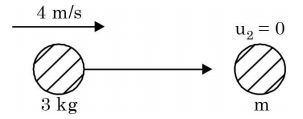
Conservation of linear momentum,
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
⇒ u₂ = 0
3 × 4 = 3 × v₁ + mv₂ ...(i)
∵ Coefficient of restitution, e = 1 for perfectly elastic collision,
v₂ – v₁ = (u₁ – u₂)
⇒ v₂ – v₁ = u₁ = 4
⇒ v₂ – v₁ = 4 ...(ii)
Conservation of energy,

1	m₁u²₁ +	1	m₂u²₂ =	1	m₁v²₁ +	1	m₂v²₂
2		2		2		2

⇒	1	× 3 × (4)² + 0 = 6 +	1	m₂v²₂
	2		2

⇒ (24 - 6)2 = m₂v²₂
⇒ mv²₂ = 36 ...(iii)
∵ v₁ = v₂ – 4
Putting in equation (i)
⇒ 12 = 3v₂ – 12 + mv₂
⇒ v₂ (3 + m) = 24 ...(iv)
Putting in equation (iii),

&RArr;		24		²	= 36
		3 + m

⇒ (3 + m)² = 16m
⇒ 9 + m² + 6m – 16m = 0
⇒ m² – 10m + 9 = 0
⇒ m² – 9m – m + 9 = 0
(m – 9)(m – 1) = 0
m = 1,9 kg