-
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels 5 km per hr. faster than the second train. If after two hours they are 50 km apart, find the average speed of faster train.
-
- 18 kmph
- 15 kmph
- 20 kmph
- 25 kmph
Correct Option: C
Let the speed of the second train be x km per hr. Then the speed of the first train is x + 5 km per hr.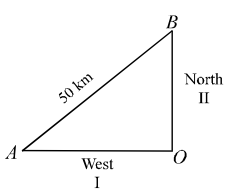
Let O be the position of the railway station from which the two trains leave. Distance travelled by the first train in 2 hours = OA = 2 (x + 5) km.
Distance travelled by the 2nd train in 2 hours= OB = 2x km.
By Pythagoras theorem,
AB2 + OA2 + OB2
⇒ 502 = [2 (x + 5)]2 + [2x]2
⇒ 2500 = 4 (x + 5)2 + 4x2
⇒ 2500 = 4 (x2 + 10x + 25) + 4x2
⇒ 8x2 + 40x – 2400 = 0
⇒ x2 + 5x – 300 = 0
⇒ x2 + 20x – 15x – 300 = 0
⇒ x (x + 20) – 15 (x + 20) = 0
⇒ (x – 15) (x + 20) = 0
⇒ x = 15, – 20
But x cannot be negative
∴ x = 15
∴ The speed of the second train is 15 km per hr. and the speed of the first train is 20 km per hr.

