-
From any point inside an equilateral triangle, the lengths of perpendiculars on the sides are ‘a’ cm, ‘b’ cm and ‘c’ cms. Its area (in cm2) is
-
-
3 (a + b + c) 3 -
√2 (a + b + c)² 3 -
√2 (a + b + c) 3 -
√2 (a + b + c)² 3
-
Correct Option: B
Using Rule 1 and 6, 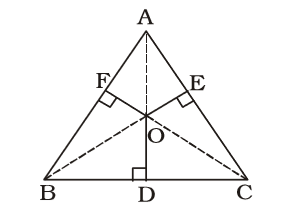
OD = a cm., OE = b cm.
OF = c cm.
BC = AC = AB
Area of ∆ABC = Area of (∆BOC + ∆COE + ∆BOA)
| = | × BC × a + | AC × b + | × AB × c | |||
| 2 | 2 | 2 |
| = | BC(a + b + c)..........(i) | |
| 2 |
(∵ AB = BC = CA)
Again, Area of ∆ABC
| = | × BC² | |
| 4 |
| ∴ | × BC² = | BC(a + b + c) | ||
| 4 | 2 |
| ⇒ BC = | (a + b + c) | |
| √3 |
| ∴ Required area = | × | (a + b + c)² | ||
| 2 | √3 |
| = | (a + b + c) | |
| √3 × √3 |
| = | (a + b + c) sq. units. | |
| 3 |