-
A, B and C together hold a pasture for which they pay a rent at the rate of $ 160 per month. They put on it 70, 50 and 40 cows respectively. A sells (2 / 7) th of his stock to B after 4 months and further 3 months later C sells (2 / 5) th of his stock to A. How much of the rent should A pay in one year?
-
- $ 500
- $ 400
- $ 760
- $ 560
Correct Option: C
On the basis of given details in question ,
Total rent to be paid for one year = 160 × 12 = $ 1920.
This is a case of compound partnership. So, the rent will be shared in proportion to the product of number of cows and time for each partner.
Computing in terms of 1 month,
For A :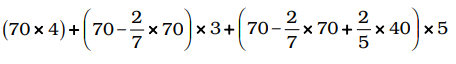
For A = (70 × 4) + (50 × 3) + (66 × 5) = 280 + 150 + 330
For A = 760
For B :
For B = 200 + 560 = 760
For C :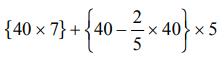
For C = 280 + 120 = 400
So, A : B : C = 760 : 760 : 400
A : B : C = 19 : 19 : 10
Sum of ratios = 19 + 19 + 10 = 48
| Rent to be paid = | = | = $ 40 | 19 + 19 + 10 | 48 |
Rent to be paid, by A = 19 × 40 = $ 760

