-
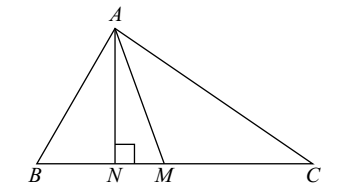
In the given figure, In a Δ ABC , ∠B = ∠ C. If AM is the bisector of ∠ BAC and AN ⊥ BC, then ∠ MAN is equal to :
-
-
1 (∠B + ∠C) 2 -
1 (∠C- ∠B ) 2 - ∠B + ∠C
-
1 (∠B - ∠C) 2 - None of these
-
Correct Option: D
In a ΔABC, ( Given ) ∠B = ∠C
Since AM is the bisector of ∠A,
| ∴ ∠MAB = | 1 | ∠A .............. ( 1 ) |
| 2 |
In right-angled ΔANB, we have: ∠B + ∠NAB = 90° ⇒ ∠NAB = 90° − ∠B ….......... (2)
∴ ∠MAN = ∠MAB - ∠NAB
| ⇒ ∠MAN = | 1 | ∠A - (90° - ∠B) |
| 2 |
| ⇒ ∠MAN = | 1 | ∠A - 90° + ∠B |
| 2 |
| ⇒ ∠MAN = | 1 | ∠A - | 1 | (∠A + ∠B + ∠C) + ∠B |
| 2 | 2 |
we know that  | ∴ | 1 | (∠A + ∠B + ∠C) = 90° |  |
| 2 |
| ⇒ ∠MAN = | 1 | ∠B - | 1 | (∠B + ∠C) |
| 2 | 2 |
| ⇒ ∠MAN = | 1 | (∠B - ∠C) |
| 2 |

